funkcja Greena,
mat. funkcja służąca do wyznaczania rozwiązań zagadnień brzegowych i początkowych dla równań różniczkowych zwyczajnych i cząstkowych;
funkcja Greena
Encyklopedia PWN
f.G. jest jądrem operatora całkowego odwrotnego do operatora różniczkowego (operator, mat. ) wyznaczonego przez dane równanie jednorodne warunki brzegowe lub brzegowo-początkowe; np. dla laplasjanu 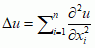 z warunkiem brzegowym Dirichleta w obszarze Ω ⊂ ℝn, dla n > 2, f.G. jest dana wzorem G(x, y) =
z warunkiem brzegowym Dirichleta w obszarze Ω ⊂ ℝn, dla n > 2, f.G. jest dana wzorem G(x, y) = 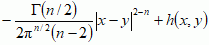 jest pewną funkcją harmoniczną, Γ(a) — funkcją gamma Eulera, a wzór u(x) = ∫ΩG(x, y)f(y)dy określa to rozwiązanie u równania △u = f, które znika na brzegu obszaru Ω.
jest pewną funkcją harmoniczną, Γ(a) — funkcją gamma Eulera, a wzór u(x) = ∫ΩG(x, y)f(y)dy określa to rozwiązanie u równania △u = f, które znika na brzegu obszaru Ω.
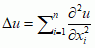 z warunkiem brzegowym Dirichleta w obszarze Ω ⊂ ℝn, dla n > 2, f.G. jest dana wzorem G(x, y) =
z warunkiem brzegowym Dirichleta w obszarze Ω ⊂ ℝn, dla n > 2, f.G. jest dana wzorem G(x, y) = 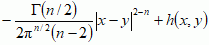 jest pewną funkcją harmoniczną, Γ(a) — funkcją gamma Eulera, a wzór u(x) = ∫ΩG(x, y)f(y)dy określa to rozwiązanie u równania △u = f, które znika na brzegu obszaru Ω.
jest pewną funkcją harmoniczną, Γ(a) — funkcją gamma Eulera, a wzór u(x) = ∫ΩG(x, y)f(y)dy określa to rozwiązanie u równania △u = f, które znika na brzegu obszaru Ω. F.G. jest ważnym narzędziem teorii równań różniczkowych, a także analizy zespolonej i teorii potencjału; oprócz tego pozwala m.in. sprowadzić poszukiwanie funkcji własnych operatorów różniczkowych do zagadnień należących do teorii równań całkowych Fredholma. Nazwa f.G. pochodzi od nazwiska G. Greena, który 1828 w swych pracach o teorii potencjału rozważał takie funkcje dla laplasjanu.


