operator
mat. funkcja przyporządkowująca elementom jednego zbioru elementy drugiego zbioru;
[łac., ‘zajmujący się czymś’, ‘wykonawca’],
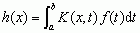 , gdzie K(x, t) jest funkcją ciągłą 2 zmiennych; występuje tu tzw. operator całkowy (K(x, t) nazywa się jego jądrem); często zarówno dziedzina, jak i zbiór zawierający zbiór wartości operatora A są przestrzeniami liniowymi (wektorowymi), np. przestrzeniami Hilberta, Banacha; ważną klasą operatorów w takich przestrzeniach są operatory liniowe; operator A jest o. liniowym, jeżeli A(αx1 + βx2) = αAx1 + βAx2, gdzie α, β — liczby, x1, x2 — dowolne elementy przestrzeni liniowej; operatorem nieliniowym jest np. operator A podnoszenia do kwadratu: Af(x) = [f(x)]2 określony na pewnym zbiorze funkcji; teorią operatorów w różnych przestrzeniach zajmuje się analiza funkcjonalna; szczególnie rozwiniętym działem teorii operatorów jest teoria operatorów w przestrzeni Hilberta, mająca ogromne znaczenie w mechanice kwantowej i w kwantowej teorii pola.
, gdzie K(x, t) jest funkcją ciągłą 2 zmiennych; występuje tu tzw. operator całkowy (K(x, t) nazywa się jego jądrem); często zarówno dziedzina, jak i zbiór zawierający zbiór wartości operatora A są przestrzeniami liniowymi (wektorowymi), np. przestrzeniami Hilberta, Banacha; ważną klasą operatorów w takich przestrzeniach są operatory liniowe; operator A jest o. liniowym, jeżeli A(αx1 + βx2) = αAx1 + βAx2, gdzie α, β — liczby, x1, x2 — dowolne elementy przestrzeni liniowej; operatorem nieliniowym jest np. operator A podnoszenia do kwadratu: Af(x) = [f(x)]2 określony na pewnym zbiorze funkcji; teorią operatorów w różnych przestrzeniach zajmuje się analiza funkcjonalna; szczególnie rozwiniętym działem teorii operatorów jest teoria operatorów w przestrzeni Hilberta, mająca ogromne znaczenie w mechanice kwantowej i w kwantowej teorii pola.