wyznacznik,
mat. dla macierzy kwadratowej A = (aij) stopnia n o składowych aij z ustalonego pierścienia przemiennego R (np. z ciała) — funkcja przyporządkowująca tej macierzy element det(A)
wyznacznik
Encyklopedia PWN
oznaczany też symbolem det A, a definiowany wzorem:
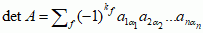 , (∗)
, (∗)
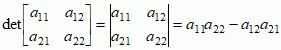 ; dla wyznacznika stopnia trzeciego
; dla wyznacznika stopnia trzeciego
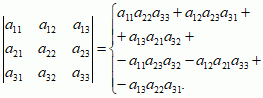
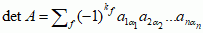 , (∗)
, (∗) w którym sumowanie odbywa się po wszystkich n! permutacjach f = α1... αn zbioru {1, ... , n}, a kf oznacza liczbę inwersji w permutacji f; w każdym składniku po prawej stronie wzoru (∗) występuje dokładnie jeden element z każdego wiersza i z każdej kolumny macierzy A; dla wyznacznika stopnia drugiego
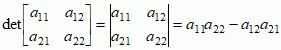 ; dla wyznacznika stopnia trzeciego
; dla wyznacznika stopnia trzeciego 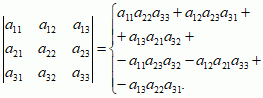
Obliczanie wyznacznika stopni wyższych niż 3 jest nieco bardziej pracochłonne: det A = ak1Ak1 + ak2Ak2 +... + akAkn, gdzie ak1, ... , akn są elementami k-tego wiersza pomnożonymi kolejno przez tzw. dopełnienia algebraiczne tych elementów (dopełnieniem algebraicznym elementu akl jest liczba Akl = (−1)k+1Mkl, gdzie Mkl jest wyznacznikiem macierzy powstałej z macierzy A przez wykreślenie w niej k-tego wiersza i l-tej kolumny; tak więc obliczenie wyznacznika stopnia n sprowadza się do obliczenia wyznacznika stopni niższych. Wyznaczniki mają wiele ciekawych własności, np.: 1) wyznacznik, w którym jakiś wiersz lub jakaś kolumna składa się z samych zer, równy jest zeru; 2) obrócenie macierzy (kwadratowej) dookoła jej głównej przekątnej o 180° nie zmienia jej wyznacznika; 3) zamiana miejscami 2 sąsiednich wierszy lub kolumn zmienia znak wyznacznika na przeciwny; 4) jeśli w macierzy wiersze lub 2 kolumny są takie same lub proporcjonalne, to wyznacznik jest równy zeru; 5) pomnożenie wiersza lub kolumny przez liczbę c sprowadza się do pomnożenia całego wyznacznika przez c; 6) det(AB) = det A · detB. Wyznaczniki znajdują szerokie zastosowanie, m.in. przy rozwiązywaniu równań liniowych.


