Fermata twierdzenie wielkie,
mat. twierdzenie teorii liczb orzekające, że dla wykładników n ≥ 3 równanie xn + yn = zn nie ma rozwiązań w liczbach całkowitych dodatnich x, y, z.
Fermata twierdzenie wielkie
Encyklopedia PWN
Twierdzenie to sformułował P. de Fermat w 1. połowie XVII w., zapisując na marginesie Arytmetyki Diofantosa, wraz z uwagą „Znalazłem zaprawdę zadziwiający dowód tego, lecz margines ten jest zbyt wąski, by go zmieścić”. Przez ponad 350 lat matematycy poszukiwali dowodu tego twierdzenia. Wielkie twierdzenie Fermata wystarczy udowodnić dla wykładników będących nieparzystymi liczbami pierwszymi, n = 3, 5, 7, 11, ... , oraz dla n = 4 (dowód w tym przypadku podał sam Fermat). Przypadek n = 3 udowodnił 1770 L. Euler; dla n = 5 i 7 dowody podali w 1. połowie XIX w. P. Dirichlet, A. Legendre i H. Lamé. W 1850 E. Kummer pierwszy udowodnił wielkie twierdzenie Fermata dla nieskończenie wielu wykładników n. Wykazał, że wielkie twierdzenie Fermata zachodzi zawsze, gdy n jest liczbą pierwszą regularną (wśród liczb pierwszych mniejszych od 100 tylko 3 nie są regularne: 37, 59 i 67).
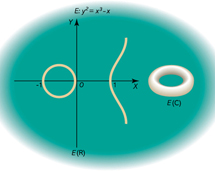
W 2. połowie XIX w. kontynuowano wysiłki, by podać dowód wielkiego twierdzenia Fermata. Problem można podzielić na 2 przypadki: Przypadek I (łatwiejszy), polegający na wykazaniu, że równanie xp + yp = zp nie ma rozwiązań x, y, z niepodzielnych przez liczbę pierwszą p, oraz Przypadek II, gdy dopuszcza się rozwiązania spełniające p|xyz (któraś z liczb x, y, z dzieli się przez p). Do końca lat 80. XX w. udało się wykazać, że Przypadek I wielkiego twierdzenia Fermata jest prawdziwy dla wykładników pierwszych p < 7 · 1017. Po podzieleniu obu stron równania Fermata przez zn otrzymuje się równanie Xp + Yp = 1 z dwiema niewiadomymi X = x/z, Y = y/z. Równanie to opisuje na płaszczyźnie tzw. krzywą Fermata. Należało udowodnić, że jedynymi punktami tej krzywej, które mają obie współrzędne wymierne, są punkty jej przecięcia z osiami układu współrzędnych. G. Faltings wykazał (1982), że krzywa ta ma co najwyżej skończenie wiele punktów wymiernych; 1986 otrzymał za to Medal Fieldsa.
Pełny dowód wielkiego twierdzenia Fermata podał 1995 A. Wiles (108 stron w „Annals of Mathematics” nr 142). W swoim dowodzie wykorzystał on inną, klasyczną rodzinę krzywych — krzywe eliptyczne. Nie dostał Medalu Fieldsa, gdyż w chwili, gdy udowodnił wielkie twierdzenie Fermata przekroczył 40. rok życia. Świat matematyczny uhonorował jego osiągnięcie specjalną plakietką (Special Tribute), wręczoną mu na Kongresie Matematycznym w Berlinie (1998). Z wielkiego twierdzenia Fermata nie wynika nic szczególnie ważnego. Niemniej jednak, praca wielu pokoleń badaczy nad jego udowodnieniem przyczyniła się do rozwoju nowych gałęzi matematyki, które dziś stosuje się do problemów często bardzo odległych od teorii liczb.
Zbigniew Marciniak