liczb teoria,
dział matematyki poświęcony badaniu liczb, początkowo naturalnych, całkowitych i wymiernych, a obecnie także algebraicznych (liczba algebraiczna).
liczb teoria
Encyklopedia PWN
Pierwszy wykład teorii liczb znajduje się w Elementach Euklidesa; Euklides wprowadził pojęcie liczby pierwszej oraz wykazał, że jest ich nieskończenie wiele. Duże znaczenie dla teorii liczb miały w starożytności prace Diofantosa (równanie diofantyczne). Za twórcę nowoczesnej teorii liczb uważa się P. Fermata; z jego nazwiskiem wiążą się 2 twierdzenia: 1) jeśli a jest liczbą naturalną, p zaś liczbą pierwszą, to liczba p dzieli liczbę ap – a (małe twierdzenie Fermata); 2) dla żadnej naturalnej liczby n > 2 równanie xn + pn = zn nie ma rozwiązań w liczbach naturalnych x, y, z (wielkie twierdzenie Fermata, ostatecznie udowodnione 1995 przez bryt. matematyka A. Wilesa). Prace Fermata z teorii liczb zapoczątkowały badania nad teorią form kwadratowych, której gł. problemem jest podanie kryteriów przedstawialności liczb całkowitych przez wartości form kwadratowych o współczynnikach całkowitych dla całkowitych wartości zmiennych. Pierwszy systematyczny wykład teorii liczb w czasach nowoż. dał A.M. Legendre 1798 (w dziele Essai sur la théorie des nombres). 
Nową epokę w teorii liczb otwierają prace C.F. Gaussa; wprowadził on pojęcie kongruencji i udowodnił 1798 podstawowe twierdzenie o kongruencjach stopnia drugiego, noszące nazwę prawa wzajemności dla reszt kwadratowych: jeżeli p oznacza liczbę pierwszą, a zaś liczbę całkowitą ≡ 0 (mod p), i jeśli oznaczyć tzw. symbolem Legendre’a 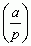 liczbę 1, gdy kongruencja x2 ≡ a (mod p) ma rozwiązania, lub liczbę –1, gdy ich nie ma, to dla dowolnych 2 różnych liczb pierwszych q, r > 2 zachodzi równość:
liczbę 1, gdy kongruencja x2 ≡ a (mod p) ma rozwiązania, lub liczbę –1, gdy ich nie ma, to dla dowolnych 2 różnych liczb pierwszych q, r > 2 zachodzi równość: 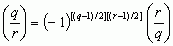 .
.
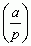 liczbę 1, gdy kongruencja x2 ≡ a (mod p) ma rozwiązania, lub liczbę –1, gdy ich nie ma, to dla dowolnych 2 różnych liczb pierwszych q, r > 2 zachodzi równość:
liczbę 1, gdy kongruencja x2 ≡ a (mod p) ma rozwiązania, lub liczbę –1, gdy ich nie ma, to dla dowolnych 2 różnych liczb pierwszych q, r > 2 zachodzi równość: 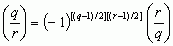 .
. W 1801 C.F. Gauss podał (w dziele Disquisitions arithmeticae) kompletną teorię arytmetyczną form kwadratowych 2 zmiennych.
Badania kontynuatorów myśli Gaussa, gł. P.G. Dirichleta, G. Eisensteina i C.G. Jacobiego, szły w kierunkach: 1) stworzenia arytmetycznej teorii form kwadratowych o dowolnej liczbie zmiennych i 2) sformułowania praw wzajemności dla reszt potęgowych wyższych stopni. Badania nad resztami potęgowymi doprowadziły do wprowadzenia uogólnienia pojęcia liczb całkowitych algebraicznych oraz pojęcia ideału. Związek teorii ideałów z teorią kongruencji algebraicznych został odkryty przez E. Kummera 1847 i ostatecznie ustalony przez J.W.R. Dedekinda. Teoria ideałów znalazła pełny wyraz w pracach J.I. Zołotariowa i L. Kroneckera. Systematyczny wykład teorii ideałów znajduje się w klas. dziele D. Hilberta Bericht über die Theorie der algebraischen Zahlen (1897). Teoria ideałów pozwoliła na sformułowanie ogólnego prawa wzajemności.
W 1. poł. XX w. powstała tzw. teoria ciał klas, będąca uwieńczeniem algebraicznej teorii liczb i korzystająca z aparatu algebry homologicznej. A. Weil zastosował do teorii liczb metody geometrii algebraicznej. W 1832 A.F. Möbius wprowadził funkcję µ(n), zw. odtąd funkcją Möbiusa (n — liczba naturalna):

Zapoczątkowało to prace nad innymi klasami funkcji liczbowych, których własności są badane m.in. metodami rachunku prawdopodobieństwa. Innymi działami teorii liczb są: teoria aproksymacji diofantycznych i geometria liczb, zapoczątkowane 1890–1909 przez H. Minkowskiego.
Matematyka pol. przyczyniła się do rozwoju teorii liczb, gł. dzięki pracom i działalności W. Sierpińskiego i jego uczniów; t.l. jest poświęcone czasopismo „Acta Arithmetica”.


