liczby naturalne,
mat. liczby 1, 2, 3, ... (niektóre definicje zaliczają do nich również 0);
liczby naturalne
Encyklopedia PWN
zbiór liczb naturalnych oznacza się symbolem ℕ; należą one do podstawowych pojęć matematyki; badania ciągu liczb naturalnych oraz działań dodawania, mnożenia, potęgowania (jak też innych funkcji na liczbach naturalnych) idą w 2 kierunkach; pierwszy dąży do wyjaśnienia natury liczb naturalnych i działań na nich, w oparciu o najprostsze pojęcia matematyki i logiki matematycznej; badania te zalicza się do podstaw matematyki; drugi kierunek zajmuje się wykrywaniem różnorodnych związków pomiędzy liczbami naturalnymi i działaniami, i zalicza się do teorii liczb. W odniesieniu do pierwszego kierunku badań na pierwszy plan wysuwa się arytmetyka teoretyczna, czyli aksjomatyczna teoria liczb naturalnych i działań; 1891 G. Peano sformułował 8 aksjomatów, z których wynikają wszystkie znane reguły arytmetyki liczb naturalnych (pierwsza próba zdefiniowania zbioru liczb naturalnych): 1) 1 ≠ x + 1; 2) jeżeli x + 1 = y + 1, to x = y; 3) aby wiedzieć, że jakaś własność przysługuje wszystkim liczbom naturalnym, wystarczy sprawdzić, że ma ją liczba 1 i że jeśli ma ją jakakolwiek liczba x, to ma ją też liczba x + 1 (tzw. aksjomat indukcji); 4) x + (y + 1) = (x + y) + 1; 5) x · 1 = x; 6) x · (y + 1) = x · y + x; 7) x1 = x; 8) xy+1 = x y · x; na podstawie tych 8 aksjomatów można definiować inne pojęcia arytmetyki, np. mówi się, że x jest mniejsze od y, symbolicznie x < y, jeżeli istnieje liczba naturalna z taka, że x + z = y.
Współczesne podstawy matematyki wychodzą od pojęcia zbioru — teorią aksjomatyczną, w której można rozwijać dedukcyjnie całą matematykę, jest teoria mnogości; w niej można zdefiniować liczby naturalne i działania x + y, x · y, xy oraz udowodnić podane wyżej aksjomaty arytmetyki; każdemu zbiorowi (skończonemu lub nieskończonemu) przyporządkowuje się liczbę kardynalną i dowodzi się, że liczba ta zależy tylko od liczebności zbioru; w ten sposób uzyskuje się konstrukcję pojęcia liczby, wychodzącą od pojęcia zbioru; liczby naturalne są to więc skończone liczby kardynalne. Pewne liczby naturalne wyróżnia się ze względu na ich interesujące własności lub znaczenie praktyczne; np. szczególnie ważną grupę liczb naturalnych stanowią liczby pierwsze; liczby bliźniacze, pary liczb pierwszych różniących się o 2, np. 3 i 5, 17 i 19, 101 i 103; nie wiadomo dotychczas, czy takich par jest nieskończenie wiele; liczby doskonałe, liczby równe sumie wszystkich dzielników mniejszych od nich samych; np. 6 (1 + 2 + 3 = 6), 28 (1 + 2 + 4 + 7 + 14 = 28); dotychczas znanych jest 41 liczb doskonałych parzystych (nie wiadomo, czy istnieją nieparzyste liczby doskonałe); wszystkie liczby doskonałe parzyste są postaci 2p–1(2p –1), gdzie 2p–1 jest liczbą pierwszą (dla p = 2 otrzymuje się 6, dla p = 3 otrzymuje się 28, największą znaną liczbę doskonałą otrzymuje się dla p = 24 036 583); liczby Fermata, liczby postaci 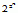 + 1 (n = 0, 1, 2, 3,...); C.F. Gauss udowodnił, że na to, by można było zbudować za pomocą cyrkla i linijki n-kąt foremny, potrzeba i wystarcza, żeby n było iloczynem potęgi liczby 2 (o wykładniku ≥ 0) i różnych liczb pierwszych będących liczbami Fermata; dotychczas znanych jest 5 liczb Fermata pierwszych i ponad 80 złożonych; liczby Mersenne’a, liczby postaci 2n –1 (n = 1, 2, 3,...); jak dotąd nie wiadomo, czy wśród liczb Mersenne’a jest nieskończenie wiele liczb pierwszych, chociaż największe znane liczby pierwsze są liczbami Mersenne’a; nazwane od nazwiska uczonego francuskieg M. Mersenne’a (1588–1648), który je badał; liczby piramidalne, liczby postaci
+ 1 (n = 0, 1, 2, 3,...); C.F. Gauss udowodnił, że na to, by można było zbudować za pomocą cyrkla i linijki n-kąt foremny, potrzeba i wystarcza, żeby n było iloczynem potęgi liczby 2 (o wykładniku ≥ 0) i różnych liczb pierwszych będących liczbami Fermata; dotychczas znanych jest 5 liczb Fermata pierwszych i ponad 80 złożonych; liczby Mersenne’a, liczby postaci 2n –1 (n = 1, 2, 3,...); jak dotąd nie wiadomo, czy wśród liczb Mersenne’a jest nieskończenie wiele liczb pierwszych, chociaż największe znane liczby pierwsze są liczbami Mersenne’a; nazwane od nazwiska uczonego francuskieg M. Mersenne’a (1588–1648), który je badał; liczby piramidalne, liczby postaci 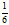 n(n + 1) (n + 2), gdzie n = 1, 2, 3,... (1, 4, 10, 20, 35,...) — odpowiada to liczbie kul, jaką można ułożyć w piramidkę czworościenną; liczby pitagorejskie, trójki liczb naturalnych x, y, z spełniające równanie x2 + y2 = z2, np. 3, 4, 5 (32 + 42 = 52) lub 5, 12, 13 (52 + 122 = 132); liczby pitagorejskie są określone ogólnymi wzorami x = d(m2 –n2), y = 2dmn, z = d(m2 + n2), gdzie m, n — dowolne względnie pierwsze liczby naturalne, a d — dowolna liczba naturalna; liczby wielokątne, liczby q-kątne, liczby określające, ile jednakowych kul można ułożyć na płaszczyźnie w kształcie wielokąta foremnego (q-kąta); n-ta (liczba kul na boku wielokąta równa n) q-kątna liczba wyraża się wzorem:
n(n + 1) (n + 2), gdzie n = 1, 2, 3,... (1, 4, 10, 20, 35,...) — odpowiada to liczbie kul, jaką można ułożyć w piramidkę czworościenną; liczby pitagorejskie, trójki liczb naturalnych x, y, z spełniające równanie x2 + y2 = z2, np. 3, 4, 5 (32 + 42 = 52) lub 5, 12, 13 (52 + 122 = 132); liczby pitagorejskie są określone ogólnymi wzorami x = d(m2 –n2), y = 2dmn, z = d(m2 + n2), gdzie m, n — dowolne względnie pierwsze liczby naturalne, a d — dowolna liczba naturalna; liczby wielokątne, liczby q-kątne, liczby określające, ile jednakowych kul można ułożyć na płaszczyźnie w kształcie wielokąta foremnego (q-kąta); n-ta (liczba kul na boku wielokąta równa n) q-kątna liczba wyraża się wzorem: 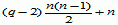 ; w szczególności dla q = 3 otrzymuje się liczby trójkątne tn = n(n –1)/2 + n = n(n + 1)/2; liczby względnie pierwsze, każde 2 liczby, które poza jednością nie mają żadnego innego wspólnego dzielnika, np.: 7 i 11, 30 i 77; liczby zaprzyjaźnione, liczby m i n spełniające następujący warunek: suma wszystkich dzielników naturalnych m (mniejszych od m) jest równa n i jednocześnie suma wszystkich dzielników naturalnych n (mniejszych od n) jest równa m; najmniejsze różne liczby zaprzyjaźnione to 220 i 284; inną parę takich liczb tworzą 1184 i 1210; w starożytności liczbom zaprzyjaźnionym przypisywano znaczenie mistyczne.
; w szczególności dla q = 3 otrzymuje się liczby trójkątne tn = n(n –1)/2 + n = n(n + 1)/2; liczby względnie pierwsze, każde 2 liczby, które poza jednością nie mają żadnego innego wspólnego dzielnika, np.: 7 i 11, 30 i 77; liczby zaprzyjaźnione, liczby m i n spełniające następujący warunek: suma wszystkich dzielników naturalnych m (mniejszych od m) jest równa n i jednocześnie suma wszystkich dzielników naturalnych n (mniejszych od n) jest równa m; najmniejsze różne liczby zaprzyjaźnione to 220 i 284; inną parę takich liczb tworzą 1184 i 1210; w starożytności liczbom zaprzyjaźnionym przypisywano znaczenie mistyczne.
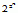 + 1 (n = 0, 1, 2, 3,...); C.F. Gauss udowodnił, że na to, by można było zbudować za pomocą cyrkla i linijki n-kąt foremny, potrzeba i wystarcza, żeby n było iloczynem potęgi liczby 2 (o wykładniku ≥ 0) i różnych liczb pierwszych będących liczbami Fermata; dotychczas znanych jest 5 liczb Fermata pierwszych i ponad 80 złożonych; liczby Mersenne’a, liczby postaci 2n –1 (n = 1, 2, 3,...); jak dotąd nie wiadomo, czy wśród liczb Mersenne’a jest nieskończenie wiele liczb pierwszych, chociaż największe znane liczby pierwsze są liczbami Mersenne’a; nazwane od nazwiska uczonego francuskieg M. Mersenne’a (1588–1648), który je badał; liczby piramidalne, liczby postaci
+ 1 (n = 0, 1, 2, 3,...); C.F. Gauss udowodnił, że na to, by można było zbudować za pomocą cyrkla i linijki n-kąt foremny, potrzeba i wystarcza, żeby n było iloczynem potęgi liczby 2 (o wykładniku ≥ 0) i różnych liczb pierwszych będących liczbami Fermata; dotychczas znanych jest 5 liczb Fermata pierwszych i ponad 80 złożonych; liczby Mersenne’a, liczby postaci 2n –1 (n = 1, 2, 3,...); jak dotąd nie wiadomo, czy wśród liczb Mersenne’a jest nieskończenie wiele liczb pierwszych, chociaż największe znane liczby pierwsze są liczbami Mersenne’a; nazwane od nazwiska uczonego francuskieg M. Mersenne’a (1588–1648), który je badał; liczby piramidalne, liczby postaci 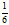 n(n + 1) (n + 2), gdzie n = 1, 2, 3,... (1, 4, 10, 20, 35,...) — odpowiada to liczbie kul, jaką można ułożyć w piramidkę czworościenną; liczby pitagorejskie, trójki liczb naturalnych x, y, z spełniające równanie x2 + y2 = z2, np. 3, 4, 5 (32 + 42 = 52) lub 5, 12, 13 (52 + 122 = 132); liczby pitagorejskie są określone ogólnymi wzorami x = d(m2 –n2), y = 2dmn, z = d(m2 + n2), gdzie m, n — dowolne względnie pierwsze liczby naturalne, a d — dowolna liczba naturalna; liczby wielokątne, liczby q-kątne, liczby określające, ile jednakowych kul można ułożyć na płaszczyźnie w kształcie wielokąta foremnego (q-kąta); n-ta (liczba kul na boku wielokąta równa n) q-kątna liczba wyraża się wzorem:
n(n + 1) (n + 2), gdzie n = 1, 2, 3,... (1, 4, 10, 20, 35,...) — odpowiada to liczbie kul, jaką można ułożyć w piramidkę czworościenną; liczby pitagorejskie, trójki liczb naturalnych x, y, z spełniające równanie x2 + y2 = z2, np. 3, 4, 5 (32 + 42 = 52) lub 5, 12, 13 (52 + 122 = 132); liczby pitagorejskie są określone ogólnymi wzorami x = d(m2 –n2), y = 2dmn, z = d(m2 + n2), gdzie m, n — dowolne względnie pierwsze liczby naturalne, a d — dowolna liczba naturalna; liczby wielokątne, liczby q-kątne, liczby określające, ile jednakowych kul można ułożyć na płaszczyźnie w kształcie wielokąta foremnego (q-kąta); n-ta (liczba kul na boku wielokąta równa n) q-kątna liczba wyraża się wzorem: 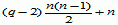 ; w szczególności dla q = 3 otrzymuje się liczby trójkątne tn = n(n –1)/2 + n = n(n + 1)/2; liczby względnie pierwsze, każde 2 liczby, które poza jednością nie mają żadnego innego wspólnego dzielnika, np.: 7 i 11, 30 i 77; liczby zaprzyjaźnione, liczby m i n spełniające następujący warunek: suma wszystkich dzielników naturalnych m (mniejszych od m) jest równa n i jednocześnie suma wszystkich dzielników naturalnych n (mniejszych od n) jest równa m; najmniejsze różne liczby zaprzyjaźnione to 220 i 284; inną parę takich liczb tworzą 1184 i 1210; w starożytności liczbom zaprzyjaźnionym przypisywano znaczenie mistyczne.
; w szczególności dla q = 3 otrzymuje się liczby trójkątne tn = n(n –1)/2 + n = n(n + 1)/2; liczby względnie pierwsze, każde 2 liczby, które poza jednością nie mają żadnego innego wspólnego dzielnika, np.: 7 i 11, 30 i 77; liczby zaprzyjaźnione, liczby m i n spełniające następujący warunek: suma wszystkich dzielników naturalnych m (mniejszych od m) jest równa n i jednocześnie suma wszystkich dzielników naturalnych n (mniejszych od n) jest równa m; najmniejsze różne liczby zaprzyjaźnione to 220 i 284; inną parę takich liczb tworzą 1184 i 1210; w starożytności liczbom zaprzyjaźnionym przypisywano znaczenie mistyczne. 

