reszt kwadratowych prawo wzajemności
Encyklopedia PWN
resztą kwadratową dla modułu p, gdzie p jest liczbą pierwszą, jest nazywana każda liczba całkowita r niepodzielna przez p, dla której kongruencja x2 ≡ r (mod p) ma rozwiązanie całkowite x, natomiast nieresztą kwadratową dla modułu p nazywa się każdą liczbę całkowitą niepodzielną przez p i nie będącą resztą kwadratową; p.w.r.k. głosi, że dla różnych liczb pierwszych nieparzystych p, q zachodzi równość 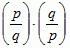 = (−1)(p-1)(q-1)/4, gdzie symbol
= (−1)(p-1)(q-1)/4, gdzie symbol 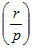 , zw. symbolem Legendre’a, przyjmuje wartość 1, gdy r jest resztą kwadratową, oraz −1, gdy r jest nieresztą kwadratową dla modułu p; np. liczba p = 67 jest resztą kwadratową dla modułu q = 7, gdyż 22 ≡ 67(mod7), a wobec tego
, zw. symbolem Legendre’a, przyjmuje wartość 1, gdy r jest resztą kwadratową, oraz −1, gdy r jest nieresztą kwadratową dla modułu p; np. liczba p = 67 jest resztą kwadratową dla modułu q = 7, gdyż 22 ≡ 67(mod7), a wobec tego 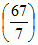 = 1, skąd na mocy p.w.r.k.
= 1, skąd na mocy p.w.r.k. 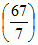 ·
· 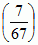 = (−1)(67-1)(7-1)/4 = (−1)99 = −1, co daje
= (−1)(67-1)(7-1)/4 = (−1)99 = −1, co daje 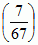 = −1, a zatem 7 jest nieresztą kwadratową dla modułu 67. P.w.r.k. zostało sformułowane po raz pierwszy przez L. Eulera (1772), a udowodnione przez C.F. Gaussa (1798 lub 1801).
= −1, a zatem 7 jest nieresztą kwadratową dla modułu 67. P.w.r.k. zostało sformułowane po raz pierwszy przez L. Eulera (1772), a udowodnione przez C.F. Gaussa (1798 lub 1801).
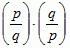 = (−1)(p-1)(q-1)/4, gdzie symbol
= (−1)(p-1)(q-1)/4, gdzie symbol 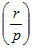 , zw. symbolem Legendre’a, przyjmuje wartość 1, gdy r jest resztą kwadratową, oraz −1, gdy r jest nieresztą kwadratową dla modułu p; np. liczba p = 67 jest resztą kwadratową dla modułu q = 7, gdyż 22 ≡ 67(mod7), a wobec tego
, zw. symbolem Legendre’a, przyjmuje wartość 1, gdy r jest resztą kwadratową, oraz −1, gdy r jest nieresztą kwadratową dla modułu p; np. liczba p = 67 jest resztą kwadratową dla modułu q = 7, gdyż 22 ≡ 67(mod7), a wobec tego 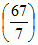 = 1, skąd na mocy p.w.r.k.
= 1, skąd na mocy p.w.r.k. 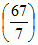 ·
· 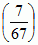 = (−1)(67-1)(7-1)/4 = (−1)99 = −1, co daje
= (−1)(67-1)(7-1)/4 = (−1)99 = −1, co daje 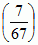 = −1, a zatem 7 jest nieresztą kwadratową dla modułu 67. P.w.r.k. zostało sformułowane po raz pierwszy przez L. Eulera (1772), a udowodnione przez C.F. Gaussa (1798 lub 1801).
= −1, a zatem 7 jest nieresztą kwadratową dla modułu 67. P.w.r.k. zostało sformułowane po raz pierwszy przez L. Eulera (1772), a udowodnione przez C.F. Gaussa (1798 lub 1801). 

