funkcje Eulera,
mat.
funkcje Eulera
Encyklopedia PWN
funkcja Eulera B (beta), funkcja specjalna określona za pomocą tzw. całki Eulera pierwszego rodzaju: 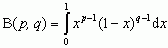 , gdzie p i q oznaczają liczby zespolone o częściach rzeczywistych większych od zera; zachodzą związki B(p, q) = B(q, p) oraz B(p, q) = Γ(p)·Γ(q)/Γ(p + q), gdzie Γ oznacza funkcję gamma Eulera;
, gdzie p i q oznaczają liczby zespolone o częściach rzeczywistych większych od zera; zachodzą związki B(p, q) = B(q, p) oraz B(p, q) = Γ(p)·Γ(q)/Γ(p + q), gdzie Γ oznacza funkcję gamma Eulera;
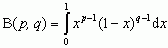 , gdzie p i q oznaczają liczby zespolone o częściach rzeczywistych większych od zera; zachodzą związki B(p, q) = B(q, p) oraz B(p, q) = Γ(p)·Γ(q)/Γ(p + q), gdzie Γ oznacza funkcję gamma Eulera;
, gdzie p i q oznaczają liczby zespolone o częściach rzeczywistych większych od zera; zachodzą związki B(p, q) = B(q, p) oraz B(p, q) = Γ(p)·Γ(q)/Γ(p + q), gdzie Γ oznacza funkcję gamma Eulera;
funkcja Eulera Γ (gamma), funkcja specjalna będąca uogólnieniem silni (silnia) — jest określona dla liczb zespolonych z o części rzeczywistej Re(z) większej od zera; zw. całką Eulera drugiego rodzaju: 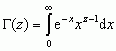 ; zachodzą związki: Γ(z + 1) = zΓ(z), Γ(z)Γ(1 − z) = π/sin πz, Γ(1/2) =
; zachodzą związki: Γ(z + 1) = zΓ(z), Γ(z)Γ(1 − z) = π/sin πz, Γ(1/2) = 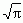 , Γ(n) = (n − 1)! dla n będącego liczbą naturalną,
, Γ(n) = (n − 1)! dla n będącego liczbą naturalną, 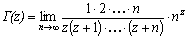 ;
;
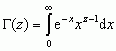 ; zachodzą związki: Γ(z + 1) = zΓ(z), Γ(z)Γ(1 − z) = π/sin πz, Γ(1/2) =
; zachodzą związki: Γ(z + 1) = zΓ(z), Γ(z)Γ(1 − z) = π/sin πz, Γ(1/2) = 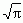 , Γ(n) = (n − 1)! dla n będącego liczbą naturalną,
, Γ(n) = (n − 1)! dla n będącego liczbą naturalną, 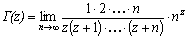 ;
;
funkcja Eulera φ(n) — funkcja wyrażająca ilość liczb naturalnych nie większych od n i względnie pierwszych z n (liczby pierwsze); np. φ(1) = 1, φ(2) = 1, φ(3) = 2, φ(4) = 2, φ(5) = 4 itd.; funkcja ta bywa nazywana też funkcją Gaussa.


