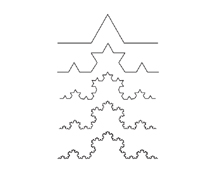
fraktal
mat. rodzaj figury geometrycznej, płaskiej lub przestrzennej, zazwyczaj charakteryzującej się własnością samopodobieństwa — małe fragmenty fraktala, oglądane w odpowiednim powiększeniu, wyglądają tak samo jak obiekt pierwotny.
[łac. fractus ‘złamany’, ‘cząstkowy’],