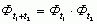układy dynamiczne,
mat. początkowo — układy równań różniczkowych opisujących ruch zgodnie z dynamiką newtonowską.
- iloczyn skalarny
- rozmaitość
- pole wektorowe
- wiązka styczna
- potok
- ergodyczna teoria
- punkt okresowy
- stabilność
- Smale’a podkowa
- atraktor
- Hausdorffa wymiar
- fraktal
- miara
- zbiór Julii
- Poincarégo twierdzenie (lemat) o powracaniu
- Liouville’a twierdzenie
- Bernoulliego układ
- bilard matematyczny
- chaos deterministyczny
- przestrzeń fazowa
- Feigenbauma parametr
- równania funkcyjne
- Julia Gaston Maurice
- katastrof teoria
- matematyka
- mieszanie
- model matematyczny
- przekształcenie
- równania różniczkowe
- Yoccoz Jean-Christophe
- przestrzeń fazowa
- miara niezmiennicza