Feigenbauma parametr

Feigenbauma parametr,

mat. wielkość charakteryzująca moment przejścia fazowego nieliniowego układu dynamicznego od zachowań regularnych (długoterminowo okresowych) do zachowań, w których mogą się pojawić stany chaotyczne (turbulencje).

W typowej jednoparametrowej rodzinie tzw. gładkich przekształceń unimodalnych, tj. z jednym „garbem” (modelowym przykładem jest rodzina f_c(x) = –x² + c), p.F. nazywa się taką wartość parametru, przy której układ ma wszystkie orbity okresowe o okresach 2ⁿ, n = 1, 2, ... , i nie ma orbit o żadnym innym okresie. Wartość p.F. zależy od konkretnej rodziny — w podanym przykładzie rodziny f_c p.F., odpowiadający zachowaniu na granicy chaosu, wynosi c = 1,401155... Amerykański fizyk M. Feigenbaum zaobserwował numerycznie, że dla szerokiej klasy układów dynamicznych przybliżanie się do granicy chaosu odbywa się według uniwersalnego, niezależnego od konkretnej rodziny schematu — wartości parametrów c_n, dla których pojawiają się stany okresowe o okresach będących kolejnymi potęgami dwójki (2ⁿ), zbliżają się do granicznego p.F. 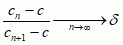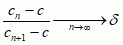w następujący sposób: , gdzie δ = 4,6692016... (stała Feigenbauma). Uniwersalny charakter przejścia układu od zachowań regularnych do chaotycznych znalazł potwierdzenie doświadczalne (pojawianie się turbulencji przy ogrzewaniu ciekłego helu) i jest wykorzystywany w modelowaniu mat., m.in. w ekonomii, biologii populacyjnej, meteorologii.

Waldemar Pałuba