stabilność,
mat. termin występujący w różnorodnych znaczeniach w wielu dziedzinach matematyki, m.in. w równaniach różniczkowych, układach dynamicznych, procesach stochastycznych, teorii gier.
stabilność
Encyklopedia PWN
W najszerszym sensie o s. mówi się wtedy, gdy rozważa się pewne obiekty, np. geom., które zależą w sposób ciągły od zmieniających się wartości parametrów. Najczęściej jednak pod pojęciem s. rozumie się własność polegającą na niewielkiej tylko zmianie przebiegu ewolucji pewnego procesu w całym, na ogół nieskończonym, przedziale czasu — gdy rozpatrywany proces rozpoczyna się w zbliżonych, tj. mało zaburzonych, warunkach początkowych lub gdy małemu zaburzeniu podlega samo prawidło (najczęściej równanie) opisujące ten proces, np. wskutek niewielkiej zmiany sił wpływających na przebieg procesu. Czasami zamiast dowolnych małych zaburzeń dopuszcza się jedynie zaburzenia spełniające pewne z góry zadane założenia. Mówi się wtedy o s. warunkowej.
Wśród różnych formalizacji s. najczęściej występuje s. w sensie Lapunowa: rozwiązanie y0(x) równania dy/dx = f(x, y), określone dla x ≥ 0, jest stabilne w sensie Lapunowa, gdy dla dowolnie małego ε > 0 istnieje δ > 0, taka że jeśli tylko |y − y0| < δ, to rozwiązanie powyższego równania z warunkiem początkowym y(x0) = y jest jednoznacznie określone dla x ≥ x0 i dla wszystkich takich x jest spełniona nierówność |y(x) − y0(x)| < ε. Dodatkowo, jeśli dla dostatecznie małych zaburzeń δ > 0 warunku początkowego jest spełniona silniejsza własność 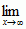 |y(x) − y0(x)| = 0, to rozwiązanie y0(x) nazywa się asymptotycznie stabilnym.
|y(x) − y0(x)| = 0, to rozwiązanie y0(x) nazywa się asymptotycznie stabilnym.
Własność s. określa się nie tylko dla pojedynczej trajektorii procesu zmiennego w czasie, ale także dla całego zespołu możliwych orbit. Prowadzi to do pojęcia s. strukturalnej. Oznacza ono zachowywanie cech jakościowych procesu (wyrażonych w pewnych własnościach tzw. portretu fazowego) przy małych zaburzeniach równania opisującego proces. W teorii układów dynamicznych występuje kilka odmiennych definicji s. strukturalnej; w najprostszej sytuacji, układu dynamicznego (&Ugot.x;, φ0) zadanego przez pojedynczy dyfeomorfizm φ0 działający na zwartej rozmaitości różniczkowej &Ugot.x;, mówi się, że układ ten (lub sam dyfeomorfizm φ0) jest strukturalnie stabilny, gdy wszystkie dyfeomorfizmy φ dostatecznie bliskie (wraz z pochodnymi) φ0 są z nim topologicznie sprzężone, tzn. istnieje homeomorfizm przestrzeni fazowej h: &Ugot.x; → &Ugot.x;, taki że φ0 = h–1 ○ φ ○ h; w przypadku układu zadanego przez potok φt z czasem ciągłym — dla równoważności portretu fazowego wymaga się, aby homeomorfizm h przeprowadzał orbity układu zaburzonego na orbity układu wyjściowego. 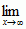 |y(x) − y0(x)| = 0, to rozwiązanie y0(x) nazywa się asymptotycznie stabilnym.
|y(x) − y0(x)| = 0, to rozwiązanie y0(x) nazywa się asymptotycznie stabilnym. Zagadnienie s. niektórych procesów pojawiło się w sposób bardzo naturalny, np. w mechanice nieba (s. ruchu planet w Układzie Słonecznym). Znalezienie kryteriów s., tj. warunków koniecznych i wystarczających dla s. danego układu, stanowiło przedmiot szeroko zakrojonych badań przez większą część XX w.; wielki wkład wnieśli do nich m.in. H. Poincaré, L. Pontriagin, A. Kołmogorow, S. Smale, W. Arnold, D. Anosow i in. Satysfakcjonujące kryteria s. znaleziono jedynie dla układów z przestrzenią fazową niskiego wymiaru (nie przekraczającego 2 dla potoków). W wyższych wymiarach problem znalezienia warunków koniecznych dla s. strukturalnej nie został do końca rozwiązany, a sama s. nie jest na ogół własnością typową (przykład Smale’a na trójwymiarowym torusie).
Waldemar Pałuba


