mieszanie

mieszanie,

mat. własność niektórych układów dynamicznych (X, T) odpowiadająca równomiernemu rozprowadzaniu (wymieszaniu) zawartości każdego typowego podzbioru przestrzeni X w całej objętości tej przestrzeni przy wielokrotnym powtarzaniu przekształcenia T. Terminem „mieszanie” nazywa się także sam układ dynamiczny mający własność m. lub działające w nim przekształcenie T. M. jest własnością silniejszą od ergodyczności, która wyraża jedynie nieistnienie istotnie mniejszego podukładu zawartego w (X, T). Intuicyjnemu pojmowaniu równomiernego rozprowadzania odpowiada następująca mat. definicja: jeśli T: X → X jest mierzalnym przekształceniem przestrzeni X w siebie, zachowującym miarę probabilistyczną P (tzn. P(T^–1(A)) = P(A) dla każdego mierzalnego podzbioru A zawartego w X), to układ (X, T) ma własność m., gdy dla wszystkich mierzalnych podzbiorów A, B (tj. tych, których prawdopodobieństwa da się określić) zachodzi równość .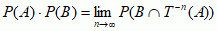

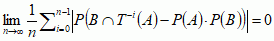Ważnym przykładem m. jest łańcuch Markowa o skończonej liczbie stanów, dla którego pewna potęga macierzy przejścia nie ma wyrazów zerowych. Własnością pośrednią między m. a ergodycznością jest m. słabe, określone warunkiem: . Dla układu dynamicznego (X, T), w którym T jest przekształceniem ciągłym, można zdefiniować m. topologiczne: T jest m. topologicznym, gdy dla dowolnych podzbiorów otwartych U, V i dla wszystkich dostatecznie dużych liczb naturalnych n zachodzi relacja T ^–n(U) ∩ V ≠ ∅.