ergodyczność

ergodyczność,

w mechanice statyst. właściwość układów dynamicznych polegająca na równości średnich czasowych funkcji (zależnych od różnych wielkości fiz.), czyli 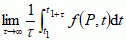obliczanych wzdłuż trajektorii fazowych układu (P oznacza punkt przestrzeni fazowej, f — dowolną gładką funkcję, t — czas, τ — interwał czasowy, po którym uśredniamy), i średnich obliczanych po odpowiednim zespole statyst. (mechanika statystyczna).

Pierwsze sformułowanie hipotezy ergodycznej dla izolowanych układów makroskopowych podał 1871 L. Boltzmann; w oryginalnej wersji postuluje ona, że średnie czasowe pewnej zmiennej w ewolucji układu mech. są równe średniej przestrzennej tej zmiennej w danej chwili czasu. Z fiz. punktu widzenia hipoteza ergodyczna oznacza, że trajektoria fazowa przechodzi z upływem czasu przez każdy punkt na hiperpowierzchni stałej energii (charakteryzującej ten układ); fakt ten wystarcza do uzasadnienia e. układu. Sens hipotezy ergodycznej jest taki, że długa obserwacja ewolucji jednego punktu dostarcza wiedzy o całym systemie, a z drugiej strony dokładna znajomość całego systemu w jednej chwili pozwala na przewidywanie średniego zachowania ewolucji dowolnego punktu w czasie. Hipoteza ergodyczna w wersji oryginalnej nie zawsze stosuje się do realnych systemów fiz., co można wykazać za pomocą eksperymentów komputerowych (m.in. E. Fermiego, Pasty i S.M. Ulama, 1955), wykazujących, że nawet w dużych nieliniowych systemach dynamicznych mogą istnieć wyraźne ślady odstępstw od e. Oryginalna hipoteza Boltzmanna została później zastąpiona przez hipotezę kwaziergodyczną P. Ehrenfesta mówiącą, że trajektoria fazowa nie przebiega przez każdy punkt hiperpowierzchni stałej energii, ale dowolnie blisko każdego punktu; sformułowanie to, chociaż fizycznie jasne, nie daje jednak konstruktywnych metod do orzekania o e. konkretnych układów.

W 1931–32 J. von Neumann i G.D. Birkhoff sformułowali mat. kryterium pozwalające stwierdzić, czy układ jest ergodyczny. Obecnie kryterium Birkhoffa jest zw. twierdzeniem ergodycznym; wynika z niego m.in., że układ dynamiczny wykazuje e. na hiperpowierzchni stałej energii (w przestrzeni fazowej), jeżeli nie ma innych niż energia całek ruchu. Ewentualne istnienie takich całek mogłoby przeszkadzać trajektoriom fazowym w swobodnym poruszaniu się po hiperpowierzchni stałej energii; jeśli jednak takie całki nie istnieją, to trajektorie fazowe mają pełną „swobodę ruchu”, co jest określane jako własność przechodniości metrycznej. W układzie ergodycznym trajektorie fazowe będą spędzać tyle samo czasu w różnych, lecz o tej samej wielkości obszarach należących do hiperpowierzchni stałej energii. Gdy eksperyment wykaże taką właściwość układu, to układ jest ergodyczny. Kryterium Birkhoffa nadal nie jest konstruktywne, jeśli chodzi o orzekanie o e. konkretnych układów.

W 1949 A. Chinczyn przeprowadził dowód e. dla pewnej ograniczonej klasy układów dynamicznych. Dla klas. gazu twardych kul dowód e. przeprowadził J.G. Sinaj. Obecnie teoria ergodyczna pozostaje gł. domeną zainteresowania matematyków. W fizyce przyjęto pragmatyczny punkt widzenia: najczęściej przyjmuje się z góry postulat o e., a słuszność przyjęcia takiego założenia jest ewentualnie (np. w późniejszych etapach obliczeń) weryfikowana przez wynikające z niego praktyczne konsekwencje.

Krzysztof Rościszewski