m topologicznym
Encyklopedia PWN
mat. zbiór X z wyróżnioną rodziną podzbiorów, nazywanych zbiorami otwartymi,
mat. pierścień (pierścień, mat. ), który jest równocześnie przestrzenią topologiczną, przy czym jego działania grupowe dodawania i mnożenia są w tej przestrzeni funkcjami ciągłymi;
topologia
mat.:
[gr. tópos ‘miejsce’, ‘okolica’, lógos ‘słowo’, ‘nauka’],
mat. dział matematyki poświęcony opisowi grup (grupa) — struktur algebraicznych najczęściej spotykanych w matematyce i jej zastosowaniach.
mat. własność niektórych układów dynamicznych (X, T) odpowiadająca równomiernemu rozprowadzaniu (wymieszaniu) zawartości każdego typowego podzbioru przestrzeni X w całej objętości tej przestrzeni przy wielokrotnym powtarzaniu przekształcenia T. Terminem „mieszanie” nazywa się także sam układ dynamiczny mający własność m. lub działające w nim przekształcenie T. M. jest własnością silniejszą od ergodyczności, która wyraża jedynie nieistnienie istotnie mniejszego podukładu zawartego w (X, T). Intuicyjnemu pojmowaniu równomiernego rozprowadzania odpowiada następująca mat. definicja: jeśli T: X → X jest mierzalnym przekształceniem przestrzeni X w siebie, zachowującym miarę probabilistyczną P (tzn. P(T–1(A)) = P(A) dla każdego mierzalnego podzbioru A zawartego w X), to układ (X, T) ma własność m., gdy dla wszystkich mierzalnych podzbiorów A, B (tj. tych, których prawdopodobieństwa da się określić) zachodzi równość 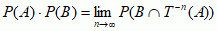 .
.
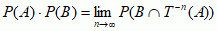 .
.


