Morse’a teoria
Encyklopedia PWN
Dla danej rozmaitości n-wymiarowej M istnieje funkcja Morse’a f: M → [0, 1] z punktami kryt. p1, ... , pk, przy czym f(p1) < f(p2) < ... < f(pk). Jeśli liczba a nie jest żadną z wartości kryt. f(pi), to podzbiór Ma = f–1(a) jest podrozmaitością M wymiaru n − 1. Jeśli b > a jest inną liczbą o tej własności, to podzbiór Ma, b = f–1[a, b] ⊂ M jest podrozmaitością z brzegiem Ma  Mb. Jeśli przedział [a, b] nie zawiera żadnej wartości kryt., to Ma, b jest po prostu walcem nad Ma = f–1(a), tj. zachodzi Ma, b ≈ Ma × [a, b]. Wybranie liczb ai, po jednej między każdą parą sąsiednich wartości kryt., powoduje, że podrozmaitości
Mb. Jeśli przedział [a, b] nie zawiera żadnej wartości kryt., to Ma, b jest po prostu walcem nad Ma = f–1(a), tj. zachodzi Ma, b ≈ Ma × [a, b]. Wybranie liczb ai, po jednej między każdą parą sąsiednich wartości kryt., powoduje, że podrozmaitości 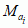 rozcinają M na podzbiory zawierające dokładnie po jednym punkcie kryt. pi. Takie podzbiory, zw. elementarnymi kobordyzmami, mają stosunkowo prostą budowę topologiczną i można je sklasyfikować. Każda rozmaitość zamknięta „jest poskładana” z pewnej liczby elementarnych kobordyzmów. Czasami prowadzi to do opisu całej rozmaitości. Na przykład, jeśli zamknięta rozmaitość M ma funkcję Morse’a z dokładnie 2 punktami kryt., to jest homeomorficzna (homeomorfizm) ze sferą (twierdzenie Reeba). Każda funkcja Morse’a prowadzi do rozkładu rozmaitości M i dlatego M ma takich rozkładów bardzo wiele. Trudność polega na rozpoznawaniu, kiedy 2 układy elementarnych kobordyzmów składają się na tę samą rozmaitość. Przy pewnych dodatkowych założeniach udaje się tę trudność pokonać. Najbardziej spektakularnym przykładem zastosowania t.M. był dowód Smale’a hipotezy Poincarégo w wymiarach n ≥ 5: każda rozmaitość zamknięta, posiadająca typ homotopii sfery Sn jest z tą sferą homeomorficzna.
rozcinają M na podzbiory zawierające dokładnie po jednym punkcie kryt. pi. Takie podzbiory, zw. elementarnymi kobordyzmami, mają stosunkowo prostą budowę topologiczną i można je sklasyfikować. Każda rozmaitość zamknięta „jest poskładana” z pewnej liczby elementarnych kobordyzmów. Czasami prowadzi to do opisu całej rozmaitości. Na przykład, jeśli zamknięta rozmaitość M ma funkcję Morse’a z dokładnie 2 punktami kryt., to jest homeomorficzna (homeomorfizm) ze sferą (twierdzenie Reeba). Każda funkcja Morse’a prowadzi do rozkładu rozmaitości M i dlatego M ma takich rozkładów bardzo wiele. Trudność polega na rozpoznawaniu, kiedy 2 układy elementarnych kobordyzmów składają się na tę samą rozmaitość. Przy pewnych dodatkowych założeniach udaje się tę trudność pokonać. Najbardziej spektakularnym przykładem zastosowania t.M. był dowód Smale’a hipotezy Poincarégo w wymiarach n ≥ 5: każda rozmaitość zamknięta, posiadająca typ homotopii sfery Sn jest z tą sferą homeomorficzna.
 Mb. Jeśli przedział [a, b] nie zawiera żadnej wartości kryt., to Ma, b jest po prostu walcem nad Ma = f–1(a), tj. zachodzi Ma, b ≈ Ma × [a, b]. Wybranie liczb ai, po jednej między każdą parą sąsiednich wartości kryt., powoduje, że podrozmaitości
Mb. Jeśli przedział [a, b] nie zawiera żadnej wartości kryt., to Ma, b jest po prostu walcem nad Ma = f–1(a), tj. zachodzi Ma, b ≈ Ma × [a, b]. Wybranie liczb ai, po jednej między każdą parą sąsiednich wartości kryt., powoduje, że podrozmaitości 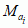 rozcinają M na podzbiory zawierające dokładnie po jednym punkcie kryt. pi. Takie podzbiory, zw. elementarnymi kobordyzmami, mają stosunkowo prostą budowę topologiczną i można je sklasyfikować. Każda rozmaitość zamknięta „jest poskładana” z pewnej liczby elementarnych kobordyzmów. Czasami prowadzi to do opisu całej rozmaitości. Na przykład, jeśli zamknięta rozmaitość M ma funkcję Morse’a z dokładnie 2 punktami kryt., to jest homeomorficzna (homeomorfizm) ze sferą (twierdzenie Reeba). Każda funkcja Morse’a prowadzi do rozkładu rozmaitości M i dlatego M ma takich rozkładów bardzo wiele. Trudność polega na rozpoznawaniu, kiedy 2 układy elementarnych kobordyzmów składają się na tę samą rozmaitość. Przy pewnych dodatkowych założeniach udaje się tę trudność pokonać. Najbardziej spektakularnym przykładem zastosowania t.M. był dowód Smale’a hipotezy Poincarégo w wymiarach n ≥ 5: każda rozmaitość zamknięta, posiadająca typ homotopii sfery Sn jest z tą sferą homeomorficzna.
rozcinają M na podzbiory zawierające dokładnie po jednym punkcie kryt. pi. Takie podzbiory, zw. elementarnymi kobordyzmami, mają stosunkowo prostą budowę topologiczną i można je sklasyfikować. Każda rozmaitość zamknięta „jest poskładana” z pewnej liczby elementarnych kobordyzmów. Czasami prowadzi to do opisu całej rozmaitości. Na przykład, jeśli zamknięta rozmaitość M ma funkcję Morse’a z dokładnie 2 punktami kryt., to jest homeomorficzna (homeomorfizm) ze sferą (twierdzenie Reeba). Każda funkcja Morse’a prowadzi do rozkładu rozmaitości M i dlatego M ma takich rozkładów bardzo wiele. Trudność polega na rozpoznawaniu, kiedy 2 układy elementarnych kobordyzmów składają się na tę samą rozmaitość. Przy pewnych dodatkowych założeniach udaje się tę trudność pokonać. Najbardziej spektakularnym przykładem zastosowania t.M. był dowód Smale’a hipotezy Poincarégo w wymiarach n ≥ 5: każda rozmaitość zamknięta, posiadająca typ homotopii sfery Sn jest z tą sferą homeomorficzna. Zbigniew Marciniak


