hesjan,
mat. forma kwadratowa 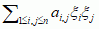 , której współczynniki aij są wartościami pochodnych cząstkowych drugiego rzędu danej funkcji f w ustalonym punkcie x,
, której współczynniki aij są wartościami pochodnych cząstkowych drugiego rzędu danej funkcji f w ustalonym punkcie x, 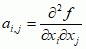 (h. funkcji n zmiennych rzeczywistych);
(h. funkcji n zmiennych rzeczywistych);
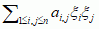 , której współczynniki aij są wartościami pochodnych cząstkowych drugiego rzędu danej funkcji f w ustalonym punkcie x,
, której współczynniki aij są wartościami pochodnych cząstkowych drugiego rzędu danej funkcji f w ustalonym punkcie x, 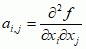 (h. funkcji n zmiennych rzeczywistych);
(h. funkcji n zmiennych rzeczywistych);