Szczególnie ważnym przykładem miary jest
miara Lebesgue’a, której konstrukcja dla zbiorów liczbowych jest następująca. Jeśli ℝ
1 oznacza przestrzeń liczb rzeczywistych, to miarą przedziału otwartego (
a,
b) lub domkniętego [
a,
b] nazywa się liczbę
b −
a (długość przedziału); zbiór pusty uważa się za przedział otwarty i przypisuje mu się miarę zero; miarę przedziału
J oznacza się symbolem |
J|; ponieważ dowolny zbiór otwarty
G można przedstawić w postaci sumy:

, gdzie
Ji ∩
Jj = ∅ dla
i ≠
j i gdzie
Ji,
Jj — przedziały otwarte, to jako miarę zbioru otwartego
G przyjmuje się liczbę
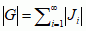
, jeśli szereg ten jest zbieżny; w przeciwnym przypadku przyjmuje się, że zbiór
G ma miarę nieskończoną: |
G| = +∞. Zbiór
A ⊂ ℝ
1 nazywa się zbiorem mierzalnym, jeżeli dla każdego
ε > 0 istnieją zbiory otwarte
G i
U, takie że
A ⊂
G,
G \
A ⊂
U i |
U| <
ε; miarę |
A| zbioru mierzalnego
A definiuje się jako kres dolny miary nadzbiorów otwartych zbioru
A: |
A| = inf {|
G|:
A ⊂
G,
G — zbiór otwarty}. Z definicji tej wynika, że zbiorami mierzalnymi są: 1) każdy zbiór otwarty; 2) suma skończonej lub przeliczalnej liczby zbiorów mierzalnych, przy czym

(równość zachodzi wtedy, gdy zbiory
An są parami rozłączne); 3) dopełnienie
Ac zbioru mierzalnego
A; 4) każdy zbiór domknięty (jako dopełnienie zbioru otwartego); 5) każdy zbiór jednopunktowy (także ma miarę zero); 6) każdy zbiór przeliczalny (ma też miarę zero), np. zbiór wszystkich liczb wymiernych; 7) każdy podzbiór zbioru miar zero również ma miarę zero. Dowodzi się, że istnieją zbiory niemierzalne, ale dowody te nie podają sposobu konstrukcji takich zbiorów; konstruując jakiś podzbiór przestrzeni ℝ
1, praktycznie można mieć pewność, że będzie to zbiór mierzalny; klasa &Mgot.x; zbiorów mierzalnych w ℝ
1 jest σ-ciałem podzbiorów przestrzeni ℝ
1.

 dla każdego ciągu (An)n = 1, 2,... podzbiorów rozłącznych ciała &Mgot.x;, to każdą taką funkcję rzeczywistą μ nazywa się miarą na σ-ciele &Mgot.x;, przy tym każdy podzbiór należący do &Mgot.x; nazywa się
dla każdego ciągu (An)n = 1, 2,... podzbiorów rozłącznych ciała &Mgot.x;, to każdą taką funkcję rzeczywistą μ nazywa się miarą na σ-ciele &Mgot.x;, przy tym każdy podzbiór należący do &Mgot.x; nazywa się  , gdzie Ji ∩ Jj = ∅ dla i ≠ j i gdzie Ji, Jj — przedziały otwarte, to jako miarę zbioru otwartego G przyjmuje się liczbę
, gdzie Ji ∩ Jj = ∅ dla i ≠ j i gdzie Ji, Jj — przedziały otwarte, to jako miarę zbioru otwartego G przyjmuje się liczbę 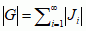 , jeśli szereg ten jest zbieżny; w przeciwnym przypadku przyjmuje się, że zbiór G ma miarę nieskończoną: |G| = +∞. Zbiór A ⊂ ℝ1 nazywa się zbiorem mierzalnym, jeżeli dla każdego ε > 0 istnieją zbiory otwarte G i U, takie że A ⊂ G, G \ A ⊂ U i |U| < ε; miarę |A| zbioru mierzalnego A definiuje się jako kres dolny miary nadzbiorów otwartych zbioru A: |A| = inf {|G|: A ⊂ G, G — zbiór otwarty}. Z definicji tej wynika, że zbiorami mierzalnymi są: 1) każdy zbiór otwarty; 2) suma skończonej lub przeliczalnej liczby zbiorów mierzalnych, przy czym
, jeśli szereg ten jest zbieżny; w przeciwnym przypadku przyjmuje się, że zbiór G ma miarę nieskończoną: |G| = +∞. Zbiór A ⊂ ℝ1 nazywa się zbiorem mierzalnym, jeżeli dla każdego ε > 0 istnieją zbiory otwarte G i U, takie że A ⊂ G, G \ A ⊂ U i |U| < ε; miarę |A| zbioru mierzalnego A definiuje się jako kres dolny miary nadzbiorów otwartych zbioru A: |A| = inf {|G|: A ⊂ G, G — zbiór otwarty}. Z definicji tej wynika, że zbiorami mierzalnymi są: 1) każdy zbiór otwarty; 2) suma skończonej lub przeliczalnej liczby zbiorów mierzalnych, przy czym  (równość zachodzi wtedy, gdy zbiory An są parami rozłączne); 3) dopełnienie Ac zbioru mierzalnego A; 4) każdy zbiór domknięty (jako dopełnienie zbioru otwartego); 5) każdy zbiór jednopunktowy (także ma miarę zero); 6) każdy zbiór przeliczalny (ma też miarę zero), np. zbiór wszystkich liczb wymiernych; 7) każdy podzbiór zbioru miar zero również ma miarę zero. Dowodzi się, że istnieją zbiory niemierzalne, ale dowody te nie podają sposobu konstrukcji takich zbiorów; konstruując jakiś podzbiór przestrzeni ℝ1, praktycznie można mieć pewność, że będzie to zbiór mierzalny; klasa &Mgot.x; zbiorów mierzalnych w ℝ1 jest σ-ciałem podzbiorów przestrzeni ℝ1.
(równość zachodzi wtedy, gdy zbiory An są parami rozłączne); 3) dopełnienie Ac zbioru mierzalnego A; 4) każdy zbiór domknięty (jako dopełnienie zbioru otwartego); 5) każdy zbiór jednopunktowy (także ma miarę zero); 6) każdy zbiór przeliczalny (ma też miarę zero), np. zbiór wszystkich liczb wymiernych; 7) każdy podzbiór zbioru miar zero również ma miarę zero. Dowodzi się, że istnieją zbiory niemierzalne, ale dowody te nie podają sposobu konstrukcji takich zbiorów; konstruując jakiś podzbiór przestrzeni ℝ1, praktycznie można mieć pewność, że będzie to zbiór mierzalny; klasa &Mgot.x; zbiorów mierzalnych w ℝ1 jest σ-ciałem podzbiorów przestrzeni ℝ1. 
