miara Jordana,
mat. miara zbudowana na wzór geom., standardowych: długości, pola, objętości (miara);
miara Jordana
Encyklopedia PWN
m.J. jest skończenie addytywna (miara sumy skończonej liczby rozłącznych zbiorów jest równa sumie ich miar), jej odpowiednikiem jest całka Riemanna (całka); w celu skonstruowania m.J. można posłużyć się ciągiem siatek dwójkowych — w przypadku 2-wymiarowym oznacza to podział płaszczyzny na kwadraty za pomocą prostych o równaniach x = n i y = m, gdzie m, n całkowite, a w następnych krokach branie kolejnych dwukrotnych zagęszczeń tego podziału; z każdą ograniczoną figurą F można związać 2 ciągi: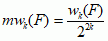 
i 
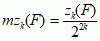, gdzie wk(F) oznacza liczbę kwadratów k-tego zagęszczenia siatki zawartych w F, a zk(F) — liczbę takich kwadratów nierozłącznych z F; każdy z tych ciągów ma granicę, zw. odpowiednio wewn. i zewnętrzną m.J. figury F; jeśli granice te są równe, to F jest mierzalna w sensie Jordana, a jej m.J. jest wspólna wartość tych granic; siatki kwadratowe można zastąpić innymi, odpowiednio dobranymi kolekcjami figur mierzalnych; analogicznie określa się m.J. dla przestrzeni innego wymiaru. Ponieważ istnieje wiele figur niemierzalnych w sensie Jordana (np. kwadrat pozbawiony punktów o współrzędnych wymiernych), a ograniczenie do skończonej addytywności powoduje wiele niedogodności przy stosowaniu m.J. w analizie mat. i rachunku prawdopodobieństwa, dlatego też m.J. często zastępuje się miarą Lebesgue’a.
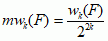i 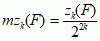, gdzie wk(F) oznacza liczbę kwadratów k-tego zagęszczenia siatki zawartych w F, a zk(F) — liczbę takich kwadratów nierozłącznych z F; każdy z tych ciągów ma granicę, zw. odpowiednio wewn. i zewnętrzną m.J. figury F; jeśli granice te są równe, to F jest mierzalna w sensie Jordana, a jej m.J. jest wspólna wartość tych granic; siatki kwadratowe można zastąpić innymi, odpowiednio dobranymi kolekcjami figur mierzalnych; analogicznie określa się m.J. dla przestrzeni innego wymiaru. Ponieważ istnieje wiele figur niemierzalnych w sensie Jordana (np. kwadrat pozbawiony punktów o współrzędnych wymiernych), a ograniczenie do skończonej addytywności powoduje wiele niedogodności przy stosowaniu m.J. w analizie mat. i rachunku prawdopodobieństwa, dlatego też m.J. często zastępuje się miarą Lebesgue’a. 
