paradoksalny rozkład kuli, paradoks (Hausdorffa–)Banacha–Tarskiego,
mat. twierdzenie, które 1924 udowodnili S. Banach i A. Tarski, uogólniając wcześniejszy przykład F. Hausdorffa;
paradoksalny rozkład kuli
Encyklopedia PWN
w ogólnej wersji orzeka, że jeśli A i B są dowolnymi podzbiorami przestrzeni euklidesowej ℝ3 o niepustych wnętrzach (np. kulami o różnych promieniach), to istnieją parami rozłączne zbiory A1, A2, ... , An, parami rozłączne zbiory B1, B2, ... , Bn oraz izometrie f1, f2, ... , fn przestrzeni ℝ3 o następujących własnościach: 1) A =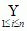 
Ai; 2) B = 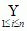Bi; 3) fi(Ai) = Bi dla wszystkich i = 1, 2, ... , n; mówiąc intuicyjnie, zbiór A można podzielić na skończoną liczbę części, z których następnie można złożyć zbiór B; z twierdzenia Banacha–Tarskiego nie wynika jednak, że dowolne otwarte podzbiory przestrzeni ℝ3 mają równe objętości: części Ai i Bi konstruuje się, wykorzystując w przemyślny sposób aksjomat wyboru; mają one tak skomplikowany kształt, że w ogóle nie można określić ich objętości (ściślej, Ai i Bi nie są zbiorami mierzalnymi w sensie miary Lebesgue’a; miara); konstrukcja Banacha i Tarskiego wykorzystuje, prócz pewnika wyboru, bogatą strukturę grupy obrotów przestrzeni (grupa przekształceń); na płaszczyźnie, gdzie grupa wszystkich izometrii jest rozwiązalna, podobny paradoks nie zachodzi: analogiczny rozkład można skonstruować jedynie wtedy, gdy zbiory A i B mają równe pola.
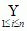Ai; 2) B = 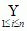Bi; 3) fi(Ai) = Bi dla wszystkich i = 1, 2, ... , n; mówiąc intuicyjnie, zbiór A można podzielić na skończoną liczbę części, z których następnie można złożyć zbiór B; z twierdzenia Banacha–Tarskiego nie wynika jednak, że dowolne otwarte podzbiory przestrzeni ℝ3 mają równe objętości: części Ai i Bi konstruuje się, wykorzystując w przemyślny sposób aksjomat wyboru; mają one tak skomplikowany kształt, że w ogóle nie można określić ich objętości (ściślej, Ai i Bi nie są zbiorami mierzalnymi w sensie miary Lebesgue’a; miara); konstrukcja Banacha i Tarskiego wykorzystuje, prócz pewnika wyboru, bogatą strukturę grupy obrotów przestrzeni (grupa przekształceń); na płaszczyźnie, gdzie grupa wszystkich izometrii jest rozwiązalna, podobny paradoks nie zachodzi: analogiczny rozkład można skonstruować jedynie wtedy, gdy zbiory A i B mają równe pola. 
