ułamek
Encyklopedia PWN
ogólniej ułamkiem nazywa się każde wyrażenie postaci 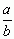 , gdzie a, b ∈ R, b ≠ 0, R — ustalony pierścień całkowity, np. pierścień liczb całkowitych; element a nazywa się licznikiem, element b — mianownikiem ułamka; ułamki a/b i c/d są równe wtedy i tylko wtedy, gdy ad = bc; sumą i różnicą ułamka a/b i c/d nazywa się odpowiednio ułamek (ad + bc)/bd i (ad – bc)/bd; iloczynem ułamka a/b i c/d nazywa się ułamek ac/bd; ułamkami są np. 1/7, 5/3, –3/5, π/4, (1 +
, gdzie a, b ∈ R, b ≠ 0, R — ustalony pierścień całkowity, np. pierścień liczb całkowitych; element a nazywa się licznikiem, element b — mianownikiem ułamka; ułamki a/b i c/d są równe wtedy i tylko wtedy, gdy ad = bc; sumą i różnicą ułamka a/b i c/d nazywa się odpowiednio ułamek (ad + bc)/bd i (ad – bc)/bd; iloczynem ułamka a/b i c/d nazywa się ułamek ac/bd; ułamkami są np. 1/7, 5/3, –3/5, π/4, (1 +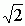 )/5 itp.; ułamek a/b, w którym a i b są liczbami całkowitymi, przedstawia liczbę wymierną. Liczbę ułamkową a/b otrzymuje się jako wynik dzielenia liczby a przez b (b ≠ 0), tzn. jako rozwiązanie x równania bx = a; ułamek a/b, w którym a i b są liczbami naturalnymi, nazywa się ułamkiem właściwym, jeżeli a < b (np. 1/7), niewłaściwym zaś, jeżeli a > b (np. 5/3); jeżeli licznik i mianownik ułamka nie mają wspólnego czynnika różnego od 1 (jak np. 3/4, 5/2), to ułamek taki nazywa się ułamkiem nieprzywiedlnym lub nieskracalnym, w przeciwnym przypadku zaś — ułamkiem przywiedlnym lub skracalnym (np. 4/12, 21/7); ułamki niewłaściwe można przedstawić jako ułamki mieszane, wydzielając z nich część całkowitą (np. 7/2 = 31/2, 5/3 = 12/3); ułamek, którego licznik lub mianownik są ułamkami, np.
)/5 itp.; ułamek a/b, w którym a i b są liczbami całkowitymi, przedstawia liczbę wymierną. Liczbę ułamkową a/b otrzymuje się jako wynik dzielenia liczby a przez b (b ≠ 0), tzn. jako rozwiązanie x równania bx = a; ułamek a/b, w którym a i b są liczbami naturalnymi, nazywa się ułamkiem właściwym, jeżeli a < b (np. 1/7), niewłaściwym zaś, jeżeli a > b (np. 5/3); jeżeli licznik i mianownik ułamka nie mają wspólnego czynnika różnego od 1 (jak np. 3/4, 5/2), to ułamek taki nazywa się ułamkiem nieprzywiedlnym lub nieskracalnym, w przeciwnym przypadku zaś — ułamkiem przywiedlnym lub skracalnym (np. 4/12, 21/7); ułamki niewłaściwe można przedstawić jako ułamki mieszane, wydzielając z nich część całkowitą (np. 7/2 = 31/2, 5/3 = 12/3); ułamek, którego licznik lub mianownik są ułamkami, np. 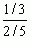 nazywa się ułamkiem piętrowym; ułamek taki można przedstawić w prostszej postaci:
nazywa się ułamkiem piętrowym; ułamek taki można przedstawić w prostszej postaci: 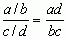 ; ułamki, których mianowniki są potęgami liczby 10 (np. 37/102, 5/10, 125/103), nazywa się ułamkami dziesiętnymi — zapisuje się je w postaci rachunkowo wygodnej, np. 37/100 = 0,37, 5/10 = 0,5, 1125/100 = 11,25; ułamkiem dziesiętnym nieskończonym nazywa się rozwinięcie dziesiętne, w którym po przecinku dziesiętnym występuje nieskończenie wiele cyfr, np. 0,102030405... , 0,333...; jeśli w rozwinięciu dziesiętnym nieskończonym pewna grupa cyfr stale się powtarza (poczynając od pewnego miejsca), to taki ułamek dziesiętny nazywa się ułamkiem dziesiętnym okresowym, przedstawia on liczbę wymierną, np. 0,333... = 1/3, 0,6727272... = 37/55; ułamki dziesiętnie nieskończone nieokresowe przedstawiają liczby rzeczywiste niewymierne, np. 2,7182818285... = e, 3,1415926536... = π, 1,4142... =
; ułamki, których mianowniki są potęgami liczby 10 (np. 37/102, 5/10, 125/103), nazywa się ułamkami dziesiętnymi — zapisuje się je w postaci rachunkowo wygodnej, np. 37/100 = 0,37, 5/10 = 0,5, 1125/100 = 11,25; ułamkiem dziesiętnym nieskończonym nazywa się rozwinięcie dziesiętne, w którym po przecinku dziesiętnym występuje nieskończenie wiele cyfr, np. 0,102030405... , 0,333...; jeśli w rozwinięciu dziesiętnym nieskończonym pewna grupa cyfr stale się powtarza (poczynając od pewnego miejsca), to taki ułamek dziesiętny nazywa się ułamkiem dziesiętnym okresowym, przedstawia on liczbę wymierną, np. 0,333... = 1/3, 0,6727272... = 37/55; ułamki dziesiętnie nieskończone nieokresowe przedstawiają liczby rzeczywiste niewymierne, np. 2,7182818285... = e, 3,1415926536... = π, 1,4142... =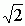 .
.
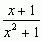 ,
, 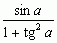 . Ułamki były znane już w starożytności (Sumerowie, Egipcjanie, Grecy, Indusi i Chińczycy); ułamki dziesiętne zostały wprowadzone pod koniec renesansu, a do podręczników szkolnych — dopiero w XVIII i XIX w.
. Ułamki były znane już w starożytności (Sumerowie, Egipcjanie, Grecy, Indusi i Chińczycy); ułamki dziesiętne zostały wprowadzone pod koniec renesansu, a do podręczników szkolnych — dopiero w XVIII i XIX w.
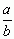 , gdzie a, b ∈ R, b ≠ 0, R — ustalony pierścień całkowity, np. pierścień liczb całkowitych; element a nazywa się licznikiem, element b — mianownikiem ułamka; ułamki a/b i c/d są równe wtedy i tylko wtedy, gdy ad = bc; sumą i różnicą ułamka a/b i c/d nazywa się odpowiednio ułamek (ad + bc)/bd i (ad – bc)/bd; iloczynem ułamka a/b i c/d nazywa się ułamek ac/bd; ułamkami są np. 1/7, 5/3, –3/5, π/4, (1 +
, gdzie a, b ∈ R, b ≠ 0, R — ustalony pierścień całkowity, np. pierścień liczb całkowitych; element a nazywa się licznikiem, element b — mianownikiem ułamka; ułamki a/b i c/d są równe wtedy i tylko wtedy, gdy ad = bc; sumą i różnicą ułamka a/b i c/d nazywa się odpowiednio ułamek (ad + bc)/bd i (ad – bc)/bd; iloczynem ułamka a/b i c/d nazywa się ułamek ac/bd; ułamkami są np. 1/7, 5/3, –3/5, π/4, (1 +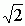 )/5 itp.; ułamek a/b, w którym a i b są liczbami całkowitymi, przedstawia liczbę wymierną. Liczbę ułamkową a/b otrzymuje się jako wynik dzielenia liczby a przez b (b ≠ 0), tzn. jako rozwiązanie x równania bx = a; ułamek a/b, w którym a i b są liczbami naturalnymi, nazywa się ułamkiem właściwym, jeżeli a < b (np. 1/7), niewłaściwym zaś, jeżeli a > b (np. 5/3); jeżeli licznik i mianownik ułamka nie mają wspólnego czynnika różnego od 1 (jak np. 3/4, 5/2), to ułamek taki nazywa się ułamkiem nieprzywiedlnym lub nieskracalnym, w przeciwnym przypadku zaś — ułamkiem przywiedlnym lub skracalnym (np. 4/12, 21/7); ułamki niewłaściwe można przedstawić jako ułamki mieszane, wydzielając z nich część całkowitą (np. 7/2 = 31/2, 5/3 = 12/3); ułamek, którego licznik lub mianownik są ułamkami, np.
)/5 itp.; ułamek a/b, w którym a i b są liczbami całkowitymi, przedstawia liczbę wymierną. Liczbę ułamkową a/b otrzymuje się jako wynik dzielenia liczby a przez b (b ≠ 0), tzn. jako rozwiązanie x równania bx = a; ułamek a/b, w którym a i b są liczbami naturalnymi, nazywa się ułamkiem właściwym, jeżeli a < b (np. 1/7), niewłaściwym zaś, jeżeli a > b (np. 5/3); jeżeli licznik i mianownik ułamka nie mają wspólnego czynnika różnego od 1 (jak np. 3/4, 5/2), to ułamek taki nazywa się ułamkiem nieprzywiedlnym lub nieskracalnym, w przeciwnym przypadku zaś — ułamkiem przywiedlnym lub skracalnym (np. 4/12, 21/7); ułamki niewłaściwe można przedstawić jako ułamki mieszane, wydzielając z nich część całkowitą (np. 7/2 = 31/2, 5/3 = 12/3); ułamek, którego licznik lub mianownik są ułamkami, np. 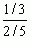 nazywa się ułamkiem piętrowym; ułamek taki można przedstawić w prostszej postaci:
nazywa się ułamkiem piętrowym; ułamek taki można przedstawić w prostszej postaci: 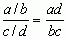 ; ułamki, których mianowniki są potęgami liczby 10 (np. 37/102, 5/10, 125/103), nazywa się ułamkami dziesiętnymi — zapisuje się je w postaci rachunkowo wygodnej, np. 37/100 = 0,37, 5/10 = 0,5, 1125/100 = 11,25; ułamkiem dziesiętnym nieskończonym nazywa się rozwinięcie dziesiętne, w którym po przecinku dziesiętnym występuje nieskończenie wiele cyfr, np. 0,102030405... , 0,333...; jeśli w rozwinięciu dziesiętnym nieskończonym pewna grupa cyfr stale się powtarza (poczynając od pewnego miejsca), to taki ułamek dziesiętny nazywa się ułamkiem dziesiętnym okresowym, przedstawia on liczbę wymierną, np. 0,333... = 1/3, 0,6727272... = 37/55; ułamki dziesiętnie nieskończone nieokresowe przedstawiają liczby rzeczywiste niewymierne, np. 2,7182818285... = e, 3,1415926536... = π, 1,4142... =
; ułamki, których mianowniki są potęgami liczby 10 (np. 37/102, 5/10, 125/103), nazywa się ułamkami dziesiętnymi — zapisuje się je w postaci rachunkowo wygodnej, np. 37/100 = 0,37, 5/10 = 0,5, 1125/100 = 11,25; ułamkiem dziesiętnym nieskończonym nazywa się rozwinięcie dziesiętne, w którym po przecinku dziesiętnym występuje nieskończenie wiele cyfr, np. 0,102030405... , 0,333...; jeśli w rozwinięciu dziesiętnym nieskończonym pewna grupa cyfr stale się powtarza (poczynając od pewnego miejsca), to taki ułamek dziesiętny nazywa się ułamkiem dziesiętnym okresowym, przedstawia on liczbę wymierną, np. 0,333... = 1/3, 0,6727272... = 37/55; ułamki dziesiętnie nieskończone nieokresowe przedstawiają liczby rzeczywiste niewymierne, np. 2,7182818285... = e, 3,1415926536... = π, 1,4142... =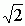 .
. Ułamkiem nazywa się również wyrażenia postaci f(x)/g(x), w których zarówno w liczniku, jak i w mianowniku występują funkcje, np.:
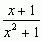 ,
, 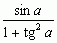 . Ułamki były znane już w starożytności (Sumerowie, Egipcjanie, Grecy, Indusi i Chińczycy); ułamki dziesiętne zostały wprowadzone pod koniec renesansu, a do podręczników szkolnych — dopiero w XVIII i XIX w.
. Ułamki były znane już w starożytności (Sumerowie, Egipcjanie, Grecy, Indusi i Chińczycy); ułamki dziesiętne zostały wprowadzone pod koniec renesansu, a do podręczników szkolnych — dopiero w XVIII i XIX w.

