częścią urojoną
Encyklopedia PWN
mat. liczba rzeczywista b w zapisie algebraicznym liczby zespolonej a + bi;
mat. liczby postaci z = a + bi, gdzie a oraz b są liczbami rzeczywistymi, nazywanymi odpowiednio częścią rzeczywistą oraz częścią urojoną z, oznaczanymi a = Re z, b = Im z, a i — jednostką urojoną, tzn. liczbą, która ma własność i2 = 
;
;
Cauchy’ego–Riemanna wzory
mat. układ równań różniczkowych cząstkowych pierwszego rzędu: ux = vy, uy = −vx, który stanowi warunek konieczny i dostateczny, by różniczkowalna w sposób ciągły funkcja zespolona f = u + iv zmiennej zespolonej z = x + iy ∈ U, gdzie U jest otwartym podzbiorem płaszczyzny zespolonej, była różniczkowalna także w sensie zespolonym (funkcje analityczne).
[w. kosziego rimanna],
mat. funkcja spełniająca równanie Laplace’a; dokładniej — funkcja rzeczywista u (określona na otwartym podzbiorze Ω przestrzeni ℝ, n ≥ 2, mająca ciągłe pochodne cząstkowe do rzędu 2. włącznie), która spełnia równanie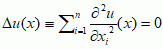 
dla wszystkich x ∈ Ω.
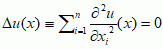dla wszystkich x ∈ Ω.
fiz. miara bezwładności drgającej części ośrodka sprężystego w układzie akustycznym, określana iloczynem gęstości i objętości ruchomego elementu tego układu;
