Cauchy’ego–Riemanna wzory

Cauchy’ego–Riemanna wzory

[w. kosziego rimanna],

mat. układ równań różniczkowych cząstkowych pierwszego rzędu: u_x = v_y, u_y = −v_x, który stanowi warunek konieczny i dostateczny, by różniczkowalna w sposób ciągły funkcja zespolona f = u + iv zmiennej zespolonej z = x + iy ∈ U, gdzie U jest otwartym podzbiorem płaszczyzny zespolonej, była różniczkowalna także w sensie zespolonym (funkcje analityczne).

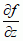Część rzeczywista u i część urojona v funkcji f spełniającej w.C.–R. są sprzężonymi funkcjami harmonicznymi — ich gradienty (u_x, u_v) i (v_x, v_v) są w każdym punkcie x + iy ∈ U prostopadłe i mają równe długości. Warunek z definicji można też zapisać inaczej:  = 0, gdzie .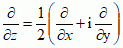