szereg Laurenta,
mat. szereg funkcyjny postaci: 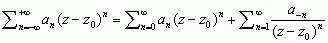 , gdzie z0 jest ustalonym punktem płaszczyzny zespolonej, a współczynniki an — liczbami zespolonymi.
, gdzie z0 jest ustalonym punktem płaszczyzny zespolonej, a współczynniki an — liczbami zespolonymi.
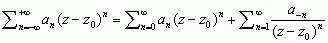 , gdzie z0 jest ustalonym punktem płaszczyzny zespolonej, a współczynniki an — liczbami zespolonymi.
, gdzie z0 jest ustalonym punktem płaszczyzny zespolonej, a współczynniki an — liczbami zespolonymi.
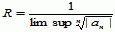 , a część osobliwa jest zbieżna na zewnątrz koła |z − z0| < r, gdzie
, a część osobliwa jest zbieżna na zewnątrz koła |z − z0| < r, gdzie 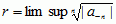 ; cały sz.L. jest więc zbieżny w pierścieniu kołowym r < |z − z0| < R, zw. pierścieniem zbieżności. Suma sz.L. przedstawia w pierścieniu zbieżności tego szeregu funkcję analityczną i na odwrót: jeżeli f(z) jest funkcją analityczną w pierścieniu r < |z − z0| < R, to f(z) daje się rozwinąć w sz.L.
; cały sz.L. jest więc zbieżny w pierścieniu kołowym r < |z − z0| < R, zw. pierścieniem zbieżności. Suma sz.L. przedstawia w pierścieniu zbieżności tego szeregu funkcję analityczną i na odwrót: jeżeli f(z) jest funkcją analityczną w pierścieniu r < |z − z0| < R, to f(z) daje się rozwinąć w sz.L. 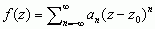 , zbieżny w tym pierścieniu, przy czym współczynniki an wyrażają się wzorami
, zbieżny w tym pierścieniu, przy czym współczynniki an wyrażają się wzorami 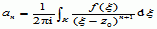 (n = 0, ±1, ±2, ...), gdzie K jest okręgiem o środku z0 i dowolnym promieniu ρ ∈ (r, R). Nazwa sz.L. pochodzi od nazwiska matematyka fr. P.A. Laurenta (1813–54), który wykazał powyższe twierdzenie. Rozwinięcia w sz.L. są uogólnieniem rozwinięć w szereg Taylora.
(n = 0, ±1, ±2, ...), gdzie K jest okręgiem o środku z0 i dowolnym promieniu ρ ∈ (r, R). Nazwa sz.L. pochodzi od nazwiska matematyka fr. P.A. Laurenta (1813–54), który wykazał powyższe twierdzenie. Rozwinięcia w sz.L. są uogólnieniem rozwinięć w szereg Taylora.