szereg potęgowy,
mat. szereg funkcyjny postaci 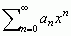 , gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
, gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
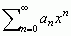 , gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
, gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
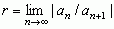 lub
lub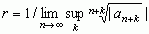 ;
;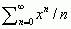 jest r = 1, dla
jest r = 1, dla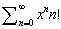 jest r = 0; przedział –r < x < + r nazywa się przedziałem zbieżności sz.p. (może być r = +∞; wtedy szereg potęgowy jest zbieżny dla wszystkich x); gdy x jest zmienną zespoloną, wtedy mówi się o kole zbieżności |x| < r, wewnątrz którego szereg potęgowy jest zbieżny, na zewnątrz zaś jest rozbieżny; szeregi potęgowe mają zastosowanie praktyczne (np. w metodach numerycznych, w fizyce, mechanice).
jest r = 0; przedział –r < x < + r nazywa się przedziałem zbieżności sz.p. (może być r = +∞; wtedy szereg potęgowy jest zbieżny dla wszystkich x); gdy x jest zmienną zespoloną, wtedy mówi się o kole zbieżności |x| < r, wewnątrz którego szereg potęgowy jest zbieżny, na zewnątrz zaś jest rozbieżny; szeregi potęgowe mają zastosowanie praktyczne (np. w metodach numerycznych, w fizyce, mechanice).