zbieżność

zbieżność,

mat. pojęcie określające sposób zachowania się wielkości zmiennej, polegający na skupianiu się jej wokół pewnej wartości;

w matematyce rozważa się rozmaite rodzaje zbieżności; mają one tę samą wspólną cechę: zbieżność ciągu elementów f_n (będących np. liczbami, funkcjami, wektorami, funkcjonałami, operatorami) do elementu granicznego f oznacza nieograniczone „zbliżanie się” elementu f_n do elementu f, czyli nieograniczone zmniejszanie się „odległości” między elementami f_n i f przy nieograniczonym zwiększaniu się liczby (wskaźnika) n (w zapisie: n → ∞); zależnie od tego, jak się zdefiniuje wzajemną odległość elementów rozważanego ciągu, otrzymuje się rozmaite rodzaje zbieżności (czyli różne definicje granicy). W szczególności w przypadku ciągu funkcyjnego f₁(x), f₂(x), ... , f_n(x)... , złożonego z funkcji określonych na wspólnym przedziale [a, b], rozróżnia się zbieżność zwyczajną (punktową) oraz zbieżność jednostajną do funkcji granicznej f(x), mianowicie: ciąg funkcyjny f_n(x) nazywa się (zwyczajnie lub punktowo) zbieżnym do funkcji granicznej f(x), dla n → ∞, jeżeli dla dowolnej dodatniej liczby ε oraz dla dowolnej liczby x z przedziału [a, b] istnieje liczba dodatnia N(ε, x), zależna od ε i od x, taka że z nierówności n > N(ε, x) wynika nierówność |f_n(x) – f(x)| < ε; jeżeli liczba N(ε) zależy jedynie od ε, ale już nie od punktu x z rozważanego przedziału, to ciąg funkcyjny f_n(x) nazywa się jednostajnie zbieżnym do funkcji granicznej f(x); w analogiczny sposób można mówić o zbieżności szeregów funkcyjnych, korzystając z pojęcia ciągu sum cząstkowych danego szeregu; ciąg funkcyjny {f_n}, określony w przedziale [a, b], nazywa się przeciętnie (średnio) zbieżnym z wykładnikiem p ≥ 1 do funkcji granicznej f(x) na przedziale [a, b], jeżeli ; 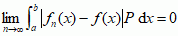najczęściej w grę wchodzą tu wykładniki p = 1 oraz p = 2; w przypadku p = 2 zamiast 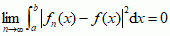pisze się skrótowo 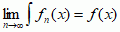(skrót lim oznacza po łacinie limes in medio, tzn. zbieżnością średnią) i mówi się po prostu o zbieżności przeciętnej. Zbieżność w dowolnej przestrzeni metrycznej M określa się następująco: dla dowolnych dwóch elementów f i g, należących do M (f, g ∈ M), definiuje się funkcję nieujemną (f, g), zwaną metryką przestrzeni; ciąg elementów f_n ∈ M nazywa się 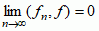zbieżnym do elementu f ∈ M, jeżeli , co się zapisuje f_n → f lub 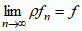; z równości 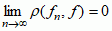wynika równość 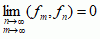, ale nie na odwrót; ciąg f_n spełniający ostatnią równość nazywa się 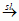ciągiem Cauchy’ego lub ciągiem podstawowym; ciąg elementów f_n ∈ H (H — przestrzeń Hilberta) nazywa się słabo zbieżnym do elementu f ∈ H (w zapisie f_n f), jeżeli dla dowolnego elementu h ∈ H zachodzi równość 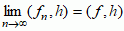, ( f, h) — iloczyn skalarny w przestrzeni Hilberta, zaś 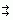mocno zbieżnym do elementu f ∈ H (w zapisie f_n → f lub f_n f), jeżeli 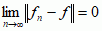, gdzie symbol ||h – f || oznacza odległość elementów h i f należących do przestrzeni Hilberta H; zbieżność mocna implikuje zbieżność słabą, ale nie na odwrót.