granica,
mat. jedno z podstawowych pojęć matematyki, spotykane przede wszystkim w szeroko rozumianej analizie matematycznej i topologii; wyraża pojmowany intuicyjnie fakt zbliżania się jakiejś wielkości do ustalonej wartości.
granica
Encyklopedia PWN
1) Granicą ciągu liczbowego a1, a2, ... , an, ... nazywa się liczbę g spełniającą warunek: dla każdego ε > 0 istnieje n0 takie, że |an –g| < ε zachodzi dla każdego n > n0; n0 jest tu liczbą, którą dobiera się do z góry zadanej liczby ε (n0 = n0(ε)); powyższy warunek oznacza, że w dowolnym przedziale — otoczeniu granicy (g – ε, g + ε), leżą prawie wszystkie wyrazy rozważanego ciągu, tzn. poza tym przedziałem znajduje się skończona liczba wyrazów, np. ciąg 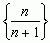 ma granicę g = 1. Jeżeli ciąg {an} ma granicę g, to fakt ten zapisuje się symbolicznie:
ma granicę g = 1. Jeżeli ciąg {an} ma granicę g, to fakt ten zapisuje się symbolicznie: 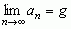 (lim, skrót łacińskiego limes ‘granica’) lub
(lim, skrót łacińskiego limes ‘granica’) lub 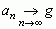 i mówi się, że ciąg {an} jest zbieżny do g. Ciąg, który nie ma granicy nazywa się rozbieżnym, np. ciąg a n = (–1)n nie ma granicy, jest więc rozbieżny.
i mówi się, że ciąg {an} jest zbieżny do g. Ciąg, który nie ma granicy nazywa się rozbieżnym, np. ciąg a n = (–1)n nie ma granicy, jest więc rozbieżny.
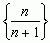 ma granicę g = 1. Jeżeli ciąg {an} ma granicę g, to fakt ten zapisuje się symbolicznie:
ma granicę g = 1. Jeżeli ciąg {an} ma granicę g, to fakt ten zapisuje się symbolicznie: 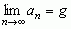 (lim, skrót łacińskiego limes ‘granica’) lub
(lim, skrót łacińskiego limes ‘granica’) lub 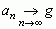 i mówi się, że ciąg {an} jest zbieżny do g. Ciąg, który nie ma granicy nazywa się rozbieżnym, np. ciąg a n = (–1)n nie ma granicy, jest więc rozbieżny.
i mówi się, że ciąg {an} jest zbieżny do g. Ciąg, który nie ma granicy nazywa się rozbieżnym, np. ciąg a n = (–1)n nie ma granicy, jest więc rozbieżny. 2) Granicą funkcji f(x) w punkcie x0 nazywa się liczbę g, jeżeli x0 jest punktem skupienia argumentów funkcji f(x) i jeżeli dla dowolnego ciągu xn argumentów zbieżnego do x0 (przy czym xn ≠ x0) zachodzi równość 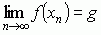 ; pisze się wówczas
; pisze się wówczas 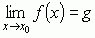 ; np.
; np. 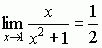 ,
, 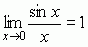 . Ścisłe określenie granicy podał 1821–23 A. Cauchy. Inne, równoważne określenie granicy funkcji podał 1880 K. Weierstrass.
. Ścisłe określenie granicy podał 1821–23 A. Cauchy. Inne, równoważne określenie granicy funkcji podał 1880 K. Weierstrass.
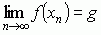 ; pisze się wówczas
; pisze się wówczas 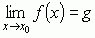 ; np.
; np. 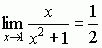 ,
, 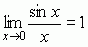 . Ścisłe określenie granicy podał 1821–23 A. Cauchy. Inne, równoważne określenie granicy funkcji podał 1880 K. Weierstrass.
. Ścisłe określenie granicy podał 1821–23 A. Cauchy. Inne, równoważne określenie granicy funkcji podał 1880 K. Weierstrass. 
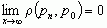 .
. 
