nieskończenie mała
Encyklopedia PWN
termin nieco staromodny, lecz wciąż dość często używany w analizie mat., a także w jej zastosowaniach w fizyce; n.m. dla x → 0 są np. funkcje: sinx, tgx, x2 i exp(−1/x2), gdyż wszystkie mają w zerze granicę równą zero; intuicyjne wyobrażenia o „tempie zbieżności do zera” uściśla się, wprowadzając pojęcie rzędu n.m.: mówi się, że n.m. f(x) jest dla x → x0 wyższego rzędu niż n.m. g(x), jeśli 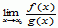 = 0; w takiej sytuacji pisze się również, że f(x) = o(g(x)) dla x → x0; natomiast jeśli są dane dwie n.m. f(x) i g(x), takie że
= 0; w takiej sytuacji pisze się również, że f(x) = o(g(x)) dla x → x0; natomiast jeśli są dane dwie n.m. f(x) i g(x), takie że 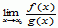 = k, przy czym |k| nie jest ani 0, ani ∞, to mówi się, że f(x) i g(x) są n.m. tego samego rzędu; np. sinx i tgx są n.m. tego samego rzędu dla x → 0, gdyż
= k, przy czym |k| nie jest ani 0, ani ∞, to mówi się, że f(x) i g(x) są n.m. tego samego rzędu; np. sinx i tgx są n.m. tego samego rzędu dla x → 0, gdyż 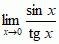 = 1, a x2 jest wyższego rzędu od każdej z nich, gdyż
= 1, a x2 jest wyższego rzędu od każdej z nich, gdyż 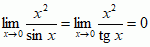 . Nazwa „nieskończenie mała” pochodzi od G.W. Leibniza, który używał jej w podobnym znaczeniu (czyniąc to, ze współcz. punktu widzenia, bardzo nieprecyzyjnie); część koncepcji Leibniza uściślił A. Robinson, twórca analizy niestandardowej.
. Nazwa „nieskończenie mała” pochodzi od G.W. Leibniza, który używał jej w podobnym znaczeniu (czyniąc to, ze współcz. punktu widzenia, bardzo nieprecyzyjnie); część koncepcji Leibniza uściślił A. Robinson, twórca analizy niestandardowej.
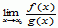 = 0; w takiej sytuacji pisze się również, że f(x) = o(g(x)) dla x → x0; natomiast jeśli są dane dwie n.m. f(x) i g(x), takie że
= 0; w takiej sytuacji pisze się również, że f(x) = o(g(x)) dla x → x0; natomiast jeśli są dane dwie n.m. f(x) i g(x), takie że 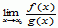 = k, przy czym |k| nie jest ani 0, ani ∞, to mówi się, że f(x) i g(x) są n.m. tego samego rzędu; np. sinx i tgx są n.m. tego samego rzędu dla x → 0, gdyż
= k, przy czym |k| nie jest ani 0, ani ∞, to mówi się, że f(x) i g(x) są n.m. tego samego rzędu; np. sinx i tgx są n.m. tego samego rzędu dla x → 0, gdyż 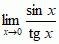 = 1, a x2 jest wyższego rzędu od każdej z nich, gdyż
= 1, a x2 jest wyższego rzędu od każdej z nich, gdyż 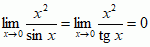 . Nazwa „nieskończenie mała” pochodzi od G.W. Leibniza, który używał jej w podobnym znaczeniu (czyniąc to, ze współcz. punktu widzenia, bardzo nieprecyzyjnie); część koncepcji Leibniza uściślił A. Robinson, twórca analizy niestandardowej.
. Nazwa „nieskończenie mała” pochodzi od G.W. Leibniza, który używał jej w podobnym znaczeniu (czyniąc to, ze współcz. punktu widzenia, bardzo nieprecyzyjnie); część koncepcji Leibniza uściślił A. Robinson, twórca analizy niestandardowej. Znaleziono w książkach Grupy PWN
Trwa wyszukiwanie... 


