zbieżny
Encyklopedia PWN
mat. szereg mający skończoną sumę S, tzn. taki, że odpowiadający mu ciąg sum częściowych {Sn} ma skończoną granicę S (Sn = a1 + a2 + ... + an);
mat. jedno z najważniejszych pojęć analizy matematycznej, pozwalające w pewnych sytuacjach nadać ścisły sens dodawaniu nieskończonej liczby składników;
mat. szereg funkcyjny postaci 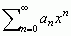 , gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
, gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
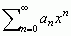 , gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
, gdzie współczynniki szeregu potęgowego an są danym ciągiem liczb, x — zmienną rzeczywistą lub zespoloną
mat. pojęcie określające sposób zachowania się wielkości zmiennej, polegający na skupianiu się jej wokół pewnej wartości;
mat. wyrażenie b1· b2 · ... · bn · ... , gdzie b1, b2, ... oznaczają liczby rzeczywiste lub zespolone;


