norma
mat. uogólnienie pojęcia wartości bezwzględnej liczby rzeczywistej i długości wektora; n. w przestrzeni liniowej X nad ciałem liczb rzeczywistych (bądź zespolonych) nazywa się każdą funkcję ∥·∥ X → ℝ spełniającą następujące trzy warunki: (1) ∥ x∥ ≥ 0 dla każdego wektora x ∈ X, przy czym ∥ x∥ = 0 wtedy i tylko wtedy, gdy x = 0 (tzn. gdy x jest wektorem zerowym), (2) ∥ tx∥ = |t| · ∥ x∥ dla każdej liczby t i każdego wektora x ∈ X, (3) ∥ x + y∥ ≤ ∥ x∥ + ∥ y∥ dla wszystkich wektorów x, y ∈ X (nierówność trójkąta);
[łac.],

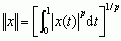 dla p ≥ 1.
dla p ≥ 1.
