funkcja Hamiltona, hamiltonian, H,
funkcja współrzędnych uogólnionych q = (q1, ... , qf), pędów uogólnionych (pęd) p = (p1, ... , pf) i ewentualnie czasu t;
funkcja Hamiltona
Encyklopedia PWN
pozwala otrzymać równania różniczkowe pierwszego rzędu opisujące całkowicie ruch układu (Hamiltona równania ruchu); jest określona wzorem:
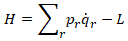 (
(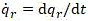 , L — funkcja Lagrange’a); funkcja Hamiltona układu o więzach niezależnych od czasu jest równa energii mech. układu; funkcję tę wprowadził 1824 W.R. Hamilton.
, L — funkcja Lagrange’a); funkcja Hamiltona układu o więzach niezależnych od czasu jest równa energii mech. układu; funkcję tę wprowadził 1824 W.R. Hamilton.
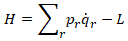 (
(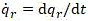 , L — funkcja Lagrange’a); funkcja Hamiltona układu o więzach niezależnych od czasu jest równa energii mech. układu; funkcję tę wprowadził 1824 W.R. Hamilton.
, L — funkcja Lagrange’a); funkcja Hamiltona układu o więzach niezależnych od czasu jest równa energii mech. układu; funkcję tę wprowadził 1824 W.R. Hamilton.

