operatory w mechanice kwantowej,
operatory odwzorowujące przestrzeń Hilberta stanów fiz. w siebie.
operatory w mechanice kwantowej
Encyklopedia PWN
Konieczność wprowadzenia o. w m.k. wynika z zupełnie innej konstrukcji mechaniki kwantowej w porównaniu z mechaniką klasyczną. Klasycznym wielkościom fiz. odpowiadają w mechanice kwantowej operatory, zw. obserwablami (np. hamiltonian — odpowiadający energii, operator położenia, pędu, momentu pędu). Obserwable są operatorami hermitowskimi o rzeczywistych wartościach własnych; stany własne obserwabli stanowią bazę zupełną przestrzeni Hilberta stanów; pomiar wielkości fiz. daje w wyniku tylko jedną z wartości własnych odpowiadającego jej operatora i przeprowadza układ w stan własny z tą wartością własną. O. w m.k. mogą mieć ciągłe lub dyskretne spektrum (wartości własne), pomiary mogą więc dawać wyniki dyskretne (np. poziomy energ. atomów) lub ciągłe (np. położenie elektronu). Ważną cechą operatorów jest ich komutowanie z innymi operatorami, np. [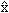 , &pcirc.x;] =
, &pcirc.x;] = 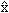 &pcirc.x; − &pcirc.x;
&pcirc.x; − &pcirc.x;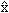 = iℏ, gdzie
= iℏ, gdzie 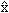 — operator położenia, &pcirc.x; — operator pędu, ℏ =
— operator położenia, &pcirc.x; — operator pędu, ℏ = 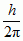 , h — stała Plancka; jeżeli komutator 2 operatorów nie znika, to nie istnieje wspólna baza stanów własnych, a stan własny jednego operatora jest superpozycją wielu stanów własnych drugiego operatora — wielkości fiz. odpowiadające tym operatorom nie mogą być na raz ściśle określone (Heisenberga zasada nieoznaczoności). Przykładem wielkości, które naraz mogą być ściśle określone, jest kwadrat momentu pędu J2 i rzut momentu pędu na wybraną oś, np. Jz, gdyż [J2, Jz] = 0. Ważnym operatorem nie będącym obserwablą jest unitarny operator ewolucji opisujący ewolucję stanów w czasie. W kwantowej teorii pola podstawową rolę odgrywają niehermitowskie operatory anihilacji i kreacji, opisujące cząstki jako wzbudzenia pola.
, h — stała Plancka; jeżeli komutator 2 operatorów nie znika, to nie istnieje wspólna baza stanów własnych, a stan własny jednego operatora jest superpozycją wielu stanów własnych drugiego operatora — wielkości fiz. odpowiadające tym operatorom nie mogą być na raz ściśle określone (Heisenberga zasada nieoznaczoności). Przykładem wielkości, które naraz mogą być ściśle określone, jest kwadrat momentu pędu J2 i rzut momentu pędu na wybraną oś, np. Jz, gdyż [J2, Jz] = 0. Ważnym operatorem nie będącym obserwablą jest unitarny operator ewolucji opisujący ewolucję stanów w czasie. W kwantowej teorii pola podstawową rolę odgrywają niehermitowskie operatory anihilacji i kreacji, opisujące cząstki jako wzbudzenia pola.
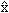 , &pcirc.x;] =
, &pcirc.x;] = 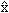 &pcirc.x; − &pcirc.x;
&pcirc.x; − &pcirc.x;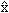 = iℏ, gdzie
= iℏ, gdzie 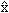 — operator położenia, &pcirc.x; — operator pędu, ℏ =
— operator położenia, &pcirc.x; — operator pędu, ℏ = 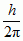 , h — stała Plancka; jeżeli komutator 2 operatorów nie znika, to nie istnieje wspólna baza stanów własnych, a stan własny jednego operatora jest superpozycją wielu stanów własnych drugiego operatora — wielkości fiz. odpowiadające tym operatorom nie mogą być na raz ściśle określone (Heisenberga zasada nieoznaczoności). Przykładem wielkości, które naraz mogą być ściśle określone, jest kwadrat momentu pędu J2 i rzut momentu pędu na wybraną oś, np. Jz, gdyż [J2, Jz] = 0. Ważnym operatorem nie będącym obserwablą jest unitarny operator ewolucji opisujący ewolucję stanów w czasie. W kwantowej teorii pola podstawową rolę odgrywają niehermitowskie operatory anihilacji i kreacji, opisujące cząstki jako wzbudzenia pola.
, h — stała Plancka; jeżeli komutator 2 operatorów nie znika, to nie istnieje wspólna baza stanów własnych, a stan własny jednego operatora jest superpozycją wielu stanów własnych drugiego operatora — wielkości fiz. odpowiadające tym operatorom nie mogą być na raz ściśle określone (Heisenberga zasada nieoznaczoności). Przykładem wielkości, które naraz mogą być ściśle określone, jest kwadrat momentu pędu J2 i rzut momentu pędu na wybraną oś, np. Jz, gdyż [J2, Jz] = 0. Ważnym operatorem nie będącym obserwablą jest unitarny operator ewolucji opisujący ewolucję stanów w czasie. W kwantowej teorii pola podstawową rolę odgrywają niehermitowskie operatory anihilacji i kreacji, opisujące cząstki jako wzbudzenia pola. 

