przestrzeń unitarna,
mat.:
przestrzeń unitarna
Encyklopedia PWN
1) unitarna przestrzeń nad ciałem liczb rzeczywistych ℝ jest to liniowa przestrzeń V nad ciałem liczb rzeczywistych ℝ, w której każdej parze wektorów α, β ∈ V jest przyporządkowana liczba rzeczywista α · β (zw. iloczynem skalarnym wektorów α i β) w taki sposób, że są spełnione następujące aksjomaty:
(1) α · β = β · α,
(2) α · (β + γ) = α · β + α · γ,
(3) (r · α) · β = r · (α · β),
(4) α · α > 0 jeśli α ≠ 0,
gdzie α, β, γ są dowolnymi wektorami z V, a r jest dowolną liczbą rzeczywistą; np. unitarnymi przestrzeniami nad ciałem liczb rzeczywistych są: kartezjańska przestrzeń m-wymiarowa ℝm z iloczynem skalarnym każdej pary punktów x = (x1, ... , xm) i y = (y1, ... , ym) określonym wzorem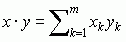 oraz przestrzeń L2 funkcji całkowalnych z kwadratem z przyjętym iloczynem skalarnym
oraz przestrzeń L2 funkcji całkowalnych z kwadratem z przyjętym iloczynem skalarnym 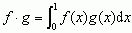 dla f, g ∈ L2.
dla f, g ∈ L2.
(1) α · β = β · α,
(2) α · (β + γ) = α · β + α · γ,
(3) (r · α) · β = r · (α · β),
(4) α · α > 0 jeśli α ≠ 0,
gdzie α, β, γ są dowolnymi wektorami z V, a r jest dowolną liczbą rzeczywistą; np. unitarnymi przestrzeniami nad ciałem liczb rzeczywistych są: kartezjańska przestrzeń m-wymiarowa ℝm z iloczynem skalarnym każdej pary punktów x = (x1, ... , xm) i y = (y1, ... , ym) określonym wzorem
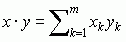 oraz przestrzeń L2 funkcji całkowalnych z kwadratem z przyjętym iloczynem skalarnym
oraz przestrzeń L2 funkcji całkowalnych z kwadratem z przyjętym iloczynem skalarnym 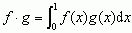 dla f, g ∈ L2.
dla f, g ∈ L2.
2) unitarna przestrzeń nad ciałem liczb zespolonych  jest to (analogicznie jak w znaczeniu 1) liniowa przestrzeń V nad ciałem liczb zespolonych
jest to (analogicznie jak w znaczeniu 1) liniowa przestrzeń V nad ciałem liczb zespolonych  , w której każdej parze wektorów α, β ∈ V jest przyporządkowana liczba zespolona α · β (iloczyn skalarny tych wektorów) spełniająca aksjomaty:
, w której każdej parze wektorów α, β ∈ V jest przyporządkowana liczba zespolona α · β (iloczyn skalarny tych wektorów) spełniająca aksjomaty:
(1′) α · β =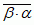 (
( oznacza liczbę sprzężoną z liczbą zespoloną c),
oznacza liczbę sprzężoną z liczbą zespoloną c),
(2)–(4) ze znaczenia 1), gdzie α, β, γ są dowolnymi wektorami z V, a r dowolną liczbą zespoloną. Oprócz symbolu α · β na oznaczanie iloczynu skalarnego wektorów α i β należących do przestrzeni unitarnej stosuje się również symbole (α, β), (α/β) lub 〈α, β〉.
 jest to (analogicznie jak w znaczeniu 1) liniowa przestrzeń V nad ciałem liczb zespolonych
jest to (analogicznie jak w znaczeniu 1) liniowa przestrzeń V nad ciałem liczb zespolonych  , w której każdej parze wektorów α, β ∈ V jest przyporządkowana liczba zespolona α · β (iloczyn skalarny tych wektorów) spełniająca aksjomaty:
, w której każdej parze wektorów α, β ∈ V jest przyporządkowana liczba zespolona α · β (iloczyn skalarny tych wektorów) spełniająca aksjomaty: (1′) α · β =
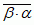 (
( oznacza liczbę sprzężoną z liczbą zespoloną c),
oznacza liczbę sprzężoną z liczbą zespoloną c), (2)–(4) ze znaczenia 1), gdzie α, β, γ są dowolnymi wektorami z V, a r dowolną liczbą zespoloną. Oprócz symbolu α · β na oznaczanie iloczynu skalarnego wektorów α i β należących do przestrzeni unitarnej stosuje się również symbole (α, β), (α/β) lub 〈α, β〉.


