Kepler Johannes  , ur. 27 XII 1571, Weil der Stadt (Wirtembergia), zm. 15 XI 1630, Ratyzbona,
, ur. 27 XII 1571, Weil der Stadt (Wirtembergia), zm. 15 XI 1630, Ratyzbona,
niemiecki astronom i matematyk.
 , ur. 27 XII 1571, Weil der Stadt (Wirtembergia), zm. 15 XI 1630, Ratyzbona,
, ur. 27 XII 1571, Weil der Stadt (Wirtembergia), zm. 15 XI 1630, Ratyzbona,
 , ur. 27 XII 1571, Weil der Stadt (Wirtembergia), zm. 15 XI 1630, Ratyzbona,
, ur. 27 XII 1571, Weil der Stadt (Wirtembergia), zm. 15 XI 1630, Ratyzbona,
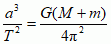 , gdzie G jest stałą grawitacji.
, gdzie G jest stałą grawitacji.