całka Lebesgue’a

całka Lebesgue’a,

mat. jedno z najważniejszych uogólnień pojęcia całki, podane 1902 przez H.L. Lebesgue’a i oparte na rozwiniętej przez niego teorii miary

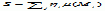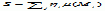jeśli obszar wartości funkcji f(x), określonej na pewnym mierzalnym zbiorze M, podzieli się punktami ... < y_–2 < y_–1 < y₀ <  y₁ < ... < y_i < ... i przez M_i oznaczy się zbiór argumentów x spełniających nierówności y_i – 1 < f(x) < y_i, a następnie utworzy się sumę , gdzie η_i — dowolna liczba z przedziału (y_i – 1, y_i), a µ(M_i) — miara zbioru M_i, to gdy istnieje granica lim S przy warunku, że największa wartość różnic y_i – 1 – y_i dąży do zera, granicę tę nazywa się całką Lebesgue’a funkcji f(x) na zbiorze M.