współrzędne kartezjańskie,
mat. uporządkowane n liczb opisujące położenie punktu w n-wymiarowej przestrzeni (układ współrzędnych).
współrzędne kartezjańskie
Encyklopedia PWN
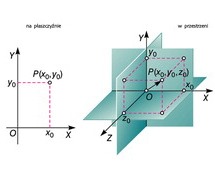
W przypadku płaszczyzny rysuje się 2 wzajemnie prostopadłe osie liczbowe przecinające się w punkcie O: jedna (zwykle pozioma) nazywa się osią odciętych, druga (zwykle pionowa) — osią rzędnych. Każdemu punktowi P tej płaszczyzny przypisuje się parę liczb (x0, y0) takich, że x0 jest co do wartości bezwzględnej równe odległości między P a jego rzutem prostokątnym na oś pionową OY, a y0 — na poziomą OX; liczba x0 jest dodatnia, gdy punkt P leży po prawej stronie osi OY, a ujemna, gdy punkt P leży po stronie lewej; podobnie liczba y0 jest dodatnia, gdy punkt P leży powyżej osi odciętych OX, a ujemna, gdy poniżej. Liczby x0, y0 nazywają się prostokątnymi współrzędnymi kartezjańskimi punktu P w układzie współrzędnych kartezjańskich OXY, przy tym x0 nazywa się odciętą, a y0 — rzędną punktu P; punkt O nazywa się początkiem układu współrzędnych kartezjańskich. Pisząc P(x0, y0) zaznacza się tym samym, że punkt P ma odciętą x0 i rzędną y0. Wektor 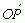 nazywa się wektorem (lub promieniem) wodzącym punktu P. Każdy punkt płaszczyzny ma 2 współrzędne kartezjańskie i na odwrót: każda para liczb x0, y0 stanowi współrzędne kartezjańskie pewnego punktu na płaszczyźnie układu OXY (a zatem ustala położenie punktu P względem osi liczbowych OX i OY). Analogicznie wprowadza się układ współrzędnych kartezjańskich w przestrzeni. Niekiedy stosuje się też ukośnokątne układy współrzędnych kartezjańskich. Współrzędne kartezjańskie są najczęściej używanymi współrzędnymi; wprowadził je P. Fermat, nazwa pochodzi od wynalazcy osi, R. Descartes’a (Kartezjusza). Pomysł jego okazał się przełomowy dla całego późniejszego rozwoju matematyki, zwłaszcza analizy matematycznej i geometrii różniczkowej.
nazywa się wektorem (lub promieniem) wodzącym punktu P. Każdy punkt płaszczyzny ma 2 współrzędne kartezjańskie i na odwrót: każda para liczb x0, y0 stanowi współrzędne kartezjańskie pewnego punktu na płaszczyźnie układu OXY (a zatem ustala położenie punktu P względem osi liczbowych OX i OY). Analogicznie wprowadza się układ współrzędnych kartezjańskich w przestrzeni. Niekiedy stosuje się też ukośnokątne układy współrzędnych kartezjańskich. Współrzędne kartezjańskie są najczęściej używanymi współrzędnymi; wprowadził je P. Fermat, nazwa pochodzi od wynalazcy osi, R. Descartes’a (Kartezjusza). Pomysł jego okazał się przełomowy dla całego późniejszego rozwoju matematyki, zwłaszcza analizy matematycznej i geometrii różniczkowej.
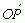 nazywa się wektorem (lub promieniem) wodzącym punktu P. Każdy punkt płaszczyzny ma 2 współrzędne kartezjańskie i na odwrót: każda para liczb x0, y0 stanowi współrzędne kartezjańskie pewnego punktu na płaszczyźnie układu OXY (a zatem ustala położenie punktu P względem osi liczbowych OX i OY). Analogicznie wprowadza się układ współrzędnych kartezjańskich w przestrzeni. Niekiedy stosuje się też ukośnokątne układy współrzędnych kartezjańskich. Współrzędne kartezjańskie są najczęściej używanymi współrzędnymi; wprowadził je P. Fermat, nazwa pochodzi od wynalazcy osi, R. Descartes’a (Kartezjusza). Pomysł jego okazał się przełomowy dla całego późniejszego rozwoju matematyki, zwłaszcza analizy matematycznej i geometrii różniczkowej.
nazywa się wektorem (lub promieniem) wodzącym punktu P. Każdy punkt płaszczyzny ma 2 współrzędne kartezjańskie i na odwrót: każda para liczb x0, y0 stanowi współrzędne kartezjańskie pewnego punktu na płaszczyźnie układu OXY (a zatem ustala położenie punktu P względem osi liczbowych OX i OY). Analogicznie wprowadza się układ współrzędnych kartezjańskich w przestrzeni. Niekiedy stosuje się też ukośnokątne układy współrzędnych kartezjańskich. Współrzędne kartezjańskie są najczęściej używanymi współrzędnymi; wprowadził je P. Fermat, nazwa pochodzi od wynalazcy osi, R. Descartes’a (Kartezjusza). Pomysł jego okazał się przełomowy dla całego późniejszego rozwoju matematyki, zwłaszcza analizy matematycznej i geometrii różniczkowej.