argumentem funkcji
Encyklopedia PWN
mat. pochodna funkcji wielu zmiennych rzeczywistych; mówi się, że funkcja f = (f1, ... , fn): ℝm → ℝn ma różniczkę zupełną Df(x) = A w punkcie x, jeśli istnieje przekształcenie liniowe A: ℝm → ℝn, takie że 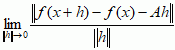 = 0;
= 0;
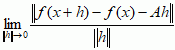 = 0;
= 0;
mat. pojęcie odnoszące się do funkcji y(x) należących do dziedziny funkcjonału J[y(x)] — w.f. y(x) oznaczona symbolem δy(x)
mat. zbiór obiektów (liczb, figur, zdań itd.), dla których dana funkcja jest określona;
jedno z najważniejszych pojęć w matematyce; precyzuje intuicje dotyczące funkcji mało zmieniającej swoje wartości przy małych zmianach argumentu (funkcja ciągła).


