wariacja funkcji,
mat. pojęcie odnoszące się do funkcji y(x) należących do dziedziny funkcjonału J[y(x)] — w.f. y(x) oznaczona symbolem δy(x)
wariacja funkcji
Encyklopedia PWN
jest to funkcja δy(x) = 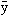 (x) – y(x), stanowiąca różnicę nowej funkcji
(x) – y(x), stanowiąca różnicę nowej funkcji 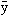 (x) i funkcji y(x) określającą przyrost (rozkład przyrostów) argumentu funkcjonału.
(x) i funkcji y(x) określającą przyrost (rozkład przyrostów) argumentu funkcjonału.
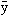 (x) – y(x), stanowiąca różnicę nowej funkcji
(x) – y(x), stanowiąca różnicę nowej funkcji 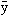 (x) i funkcji y(x) określającą przyrost (rozkład przyrostów) argumentu funkcjonału.
(x) i funkcji y(x) określającą przyrost (rozkład przyrostów) argumentu funkcjonału. Wariacja funkcji jest dla funkcjonału odpowiednikiem przyrostu zmiennej niezależnej funkcji. Pojęcie to występuje w metodzie wariacji Lagrange’a wyznaczania ekstremów funkcjonałów, stanowiącej jedną z metod wyznaczania ekstremów funkcjonałów (rachunku wariacyjnego). Istota metody Lagrange’a polega na tym, że pojęcie różniczki, za pomocą którego buduje się teorię ekstremów funkcji o skończonej liczbie zmiennych, rozszerza się na funkcjonały (wariacja funkcjonału) z zachowaniem zasady, że w punkcie ekstremum różniczka (wariacja funkcjonału) równa się zeru.


