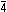symetria kryształu,
prawidłowe powtarzanie się w przestrzeni jednakowych pod względem fiz. i geom. części kryształu (ścian, krawędzi, płaszczyzn sieciowych, atomów, cząsteczek, komórek elementarnych itp.).
symetria kryształu
Encyklopedia PWN
Mówiąc inaczej, symetria jest właściwością kryształu polegającą na tym, że przy określonych zmianach położenia kryształu nowe jego położenia są nieodróżnialne od położenia wyjściowego. Takie zmiany położenia nazywa się operacjami symetrii (przekształceniami symetrycznymi). Operacje symetrii są zwykle związane z obecnością w przestrzeni pewnych nieruchomych punktów, prostych i płaszczyzn, względem których operacje są przeprowadzane, a które nazywają się elementami symetrii. Elementy symetrii dzielą się na makroskopowe (środek symetrii, osie symetrii, osie inwersyjne, płaszczyzny symetrii) oraz strukturalne, wynikające z istnienia osi translacji i makroskopowych elementów symetrii (osie śrubowe, płaszczyzny poślizgu).
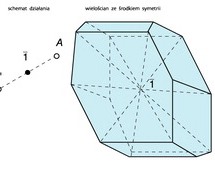
Środek symetrii, centrum symetrii (symbol międzynar. 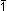 ) — punkt wewnątrz kryształu mający tę własność, że na dowolnej prostej przeprowadzonej przez ten punkt, w jednakowej od niego odległości, znajdują się jednakowe części kryształu. Związana z nim operacja symetrii — odbicie w środku symetrii (inwersja).
) — punkt wewnątrz kryształu mający tę własność, że na dowolnej prostej przeprowadzonej przez ten punkt, w jednakowej od niego odległości, znajdują się jednakowe części kryształu. Związana z nim operacja symetrii — odbicie w środku symetrii (inwersja).
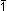 ) — punkt wewnątrz kryształu mający tę własność, że na dowolnej prostej przeprowadzonej przez ten punkt, w jednakowej od niego odległości, znajdują się jednakowe części kryształu. Związana z nim operacja symetrii — odbicie w środku symetrii (inwersja).
) — punkt wewnątrz kryształu mający tę własność, że na dowolnej prostej przeprowadzonej przez ten punkt, w jednakowej od niego odległości, znajdują się jednakowe części kryształu. Związana z nim operacja symetrii — odbicie w środku symetrii (inwersja).
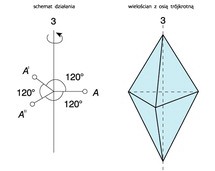
Oś symetrii, oś obrotu (symbol n) — prosta, wokół której, w jednakowej od niej odległości, powtarzają się jednakowe części kryształu; ze względu na sieciową budowę kryształu części te mogą powtarzać się jedynie co kąt α = 360°, 180°, 120°, 90°, 60°; liczbę n = 360°/α nazywa się krotnością osi; możliwe są więc w kryształach osie: 1-, 2-, 3-, 4- i 6-krotne, o symbolach odpowiednio 1, 2, 3, 4, 6. Operacja symetrii — obrót wokół osi.
Płaszczyzna symetrii, płaszczyzna zwierciadlana (symbol m) — płaszczyzna dzieląca kryształ na 2 części, pozostające względem siebie w takim stosunku, jak przedmiot do swego obrazu w płaskim zwierciadle. Operacja symetrii — odbicie w płaszczyźnie.
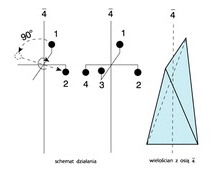
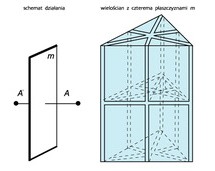
Oś inwersyjna (symbol 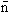 ) — złożony element symetrii, którego działanie polega na powtarzaniu się danej części kryształu po wykonaniu obrotu wokół osi symetrii o kąt α = 360°/n i odbicia w środku symetrii.; np.
) — złożony element symetrii, którego działanie polega na powtarzaniu się danej części kryształu po wykonaniu obrotu wokół osi symetrii o kąt α = 360°/n i odbicia w środku symetrii.; np. 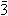 . Operacja symetrii — obrót inwersyjny.
. Operacja symetrii — obrót inwersyjny.
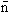 ) — złożony element symetrii, którego działanie polega na powtarzaniu się danej części kryształu po wykonaniu obrotu wokół osi symetrii o kąt α = 360°/n i odbicia w środku symetrii.; np.
) — złożony element symetrii, którego działanie polega na powtarzaniu się danej części kryształu po wykonaniu obrotu wokół osi symetrii o kąt α = 360°/n i odbicia w środku symetrii.; np. 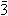 . Operacja symetrii — obrót inwersyjny.
. Operacja symetrii — obrót inwersyjny.
Oś translacji (symbol t) — prosta, wzdłuż której powtarzają się nieskończoną liczbę razy, w tej samej od siebie odległości τ, takie same fragmenty struktury kryształu; odległość τ nazywa się odcinkiem translacji lub periodem identyczności. Oś translacji jest podstawowym elementem symetrii sieci przestrzennych kryształów. Operacja symetrii — translacja (przesunięcie).
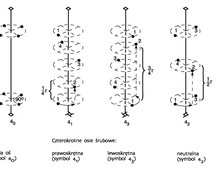
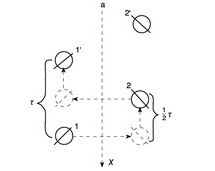
Oś śrubowa (symbol np) — złożony element symetrii, którego działanie polega na powtarzaniu się danego fragmentu struktury kryształu po wykonaniu obrotu wokół osi symetrii o kąt α = 360°/n i przesunięcia tego fragmentu w kierunku równoległym do osi symetrii o część odcinka translacji równą (p/n) · τ, gdzie p jest liczbą naturalną (p < n); pod działaniem takiej osi wszystkie części struktury przesuwają się po liniach śrubowych. W strukturach kryształów występuje 11 osi śrubowych; rozróżnia się osie śrubowe prawoskrętne (np. 41), lewoskrętne (np. 43) i neutralne, bez wyróżnionego kierunku skrętu (np. 42). Operacja symetrii — obrót śrubowy.
Płaszczyzna poślizgu (symbole a, b, c, n, d) — złożony element symetrii, którego działanie polega na powtarzaniu się danego fragmentu struktury kryształu po wykonaniu odbicia w płaszczyźnie symetrii i jednym lub dwóch przesunięciach — równoległych do płaszczyzny symetrii — o odpowiednią część odcinka translacji τ. Zależnie od wielkości i kierunku przesunięcia oraz od liczby przesunięć płaszczyzny poślizgu oznacza się: symbolem a, b lub c (1 przesunięcie o 1/2τ odpowiednio w kierunku osi X, Y lub Z), symbolem n (2 przesunięcia o 1/2τ), symbolem d (2 przesunięcia o 1/4τ). Operacja symetrii — odbicie poślizgowe.
Różne możliwe w kryształach kombinacje makroskopowych elementów symetrii tworzą 32 klasy krystalograficzne, określające symetrię zewn. postaci kryształów. Sieć przestrzenna kryształu ma te same elementy symetrii co jego postać zewn.; ponadto może mieć osie śrubowe i płaszczyzny poślizgu. Z kombinacji makroskopowych i strukturalnych elementów symetrii wynika 230 grup przestrzennych, określających symetrię wewn. budowy kryształów. Klasyczna teoria, zajmująca się klasami krystalograf. i grupami przestrzennymi, całkowicie wystarcza do jednoznacznego opisu struktur kryształów. Jednak za pomocą tej teorii nie da się przeprowadzić takiego opisu struktury, który uwzględniałby np. kierunki spinów atomów. Zmusza to do rozszerzenia pojęcia symetrii przez uwzględnienie przekształceń antysymetrycznych, tj. takich, w których każdemu przekształceniu symetrycznemu figury towarzyszy zmiana na przeciwną pewnej jej właściwości fiz. (antysymetria). Teoria klas. zawodzi również przy opisie symetrii kryształów rzeczywistych, często zdefektowanych, o nieprawidłowych postaciach (np. kryształów szkieletowych). W przypadku takich kryształów duże usługi oddają teorie symetrii krzywoliniowej (D. Naliwkin, 1925) i symetrii podobieństwa (A. Szubnikow, 1960). Symetria krzywoliniowa powstaje np. przy zginaniu zwykłych symetrycznych figur, przy czym osie symetrii i płaszczyzny symetrii przechodzą w osie i płaszczyzny krzywoliniowe. W teorii symetrii podobieństwa za jednakowe przyjmuje się wszystkie figury do siebie podobne (tj. o jednakowym kształcie), lecz różniące się wielkością; przekształceniom symetrycznym, będącym analogami translacji, odbić w płaszczyznach, obrotów wokół osi, towarzyszy równoczesne zwiększanie (lub zmniejszanie) wielkości figur i odległości między figurami.
Ilustracje