Dynkina diagramy

Dynkina diagramy,

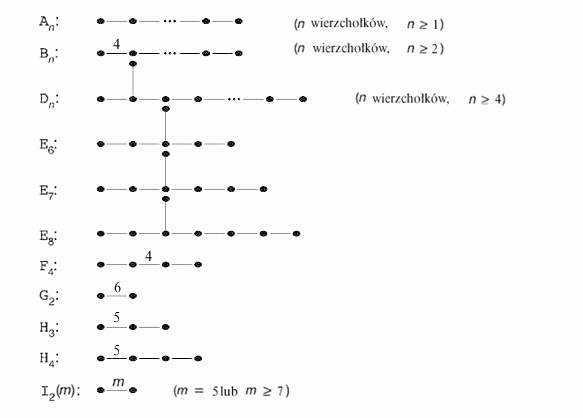
mat. klasa grafów niezorientowanych pojawiających się w problemach klasyfikacyjnych matematyki, fizyki, krystalografii, chemii i in. D.D. nazywa się każdy ze skończonych grafów przedstawionych na rysunku.

Niektóre z krawędzi tych grafów są oznaczone liczbami naturalnymi większymi od 3. Grafy typu &Adbl.x;_n, &Ddbl.x;_n, &Edbl.x;₆, &Edbl.x;₇ oraz &Edbl.x;₈, nie posiadające krawędzi oznaczonych liczbami, nazywa się jednorodnymi d.D. Stosuje się też równoważny zapis d.D., zastępując krawędzie 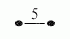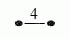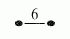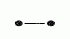, , 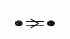, 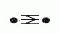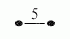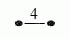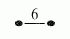odpowiednio przez , , .

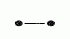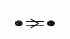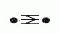Wielu matematyków zajmuje się problemem wyjaśnienia zjawiska występowania d.D. w rozwiązaniach problemów klasyfikacyjnych. Nie ma jeszcze satysfakcjonujących wyjaśnień tego zjawiska, choć geneza i wspólne źródła występowania d.D. w wielu twierdzeniach współcz. matematyki są już dobrze zrozumiane. W zakresie algebry i geometrii do takich rozwiązań (uzyskanych w XIX i XX w.) zalicza się m.in.: 1) klasyfikację skończonych grup Coxetera; 2) klasyfikację skończonych podgrup grupy izometrii trójwymiarowej przestrzeni euklidesowej; 3) klasyfikację grup symetrii wielościanów foremnych; 4) opis dodatnio określonych symetryzowalnych macierzy Cartana; 5) budowę prostych zespolonych algebr Liego; 6) klasyfikację prostych osobliwości hiperpowierzchni algebraicznych; 7) klasyfikację grup skończonych generowanych przez odbicia; 8) opis wszystkich skończonych grafów zorientowanych posiadających skończony typ reprezentacyjny.

W szczególności udowodniono, że istnieje wzajemnie jednoznaczna odpowiedniość pomiędzy d.D. oraz klasami izomorfizmu skończonych nierozkładalnych grup Coxetera, przy czym każdej grupie symetrii kryształu (kryształu symetria) odpowiada pewien d.D., który nie jest równy diagramowi typu ℍ₃, ℍ₄ lub &Idbl.x;_m.

Daniel Simson