rozkład zmiennej losowej, rozkład prawdopodobieństwa,
mat. miara prawdopodobieństwa wyznaczona przez zmienną losową w zbiorze jej możliwych wartości.
- prawdopodobieństwo
- losowa zmienna
- wartość oczekiwana
- wariancja
- test χ<SUP>2</SUP>
- test Studenta
- rozkład Bernoulliego
- błędów teoria
- centralne twierdzenie graniczne
- rozkład dwumianowy
- dystrybuanta
- fizyka statystyczna
- Galtona deska
- Gauss Carl Friedrich
- Gaussa rozkład
- rozkład geometryczny
- geostatystyka
- gęstość rozkładu
- gier teoria
- graniczne twierdzenia
- rozkład hipergeometryczny
- hipoteza statystyczna
- kurtoza
- kwantyl
- próba losowa
- mechanika statystyczna
- moment
- największej wiarygodności (wiarogodności) metoda
- rozkład normalny
- Poissona proces
- Poissona rozkład
- poziom ufności
- gęstość prawdopodobieństwa
- prawdopodobieństwa rachunek
- prawdopodobieństwa rozkład
- probit
- skośność
- tablice statystyczne
- statystyka
- stochastyczne procesy
- trzech sigm reguła
- rozkład wykładniczy
- wyrównawczy rachunek
- zmienna losowa
- korelacja

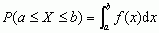 ; dla zmiennych losowych skokowych podaje się zazwyczaj zbiór możliwych wartości x1, x2, ... tej zmiennej oraz odpowiadające tym wartościom prawdopodobieństwa p1, p2, ...; rozkład prawdopodobieństwa zmiennej losowej X można również wyznaczyć przez podanie tzw. funkcji charakterystycznej, tj. funkcji φ(t) = E(eitX), gdzie: t — liczba rzeczywista, i — jednostka urojona, a E(Y) oznacza
; dla zmiennych losowych skokowych podaje się zazwyczaj zbiór możliwych wartości x1, x2, ... tej zmiennej oraz odpowiadające tym wartościom prawdopodobieństwa p1, p2, ...; rozkład prawdopodobieństwa zmiennej losowej X można również wyznaczyć przez podanie tzw. funkcji charakterystycznej, tj. funkcji φ(t) = E(eitX), gdzie: t — liczba rzeczywista, i — jednostka urojona, a E(Y) oznacza 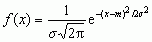 , gdzie m — wartość średnia, σ 2
, gdzie m — wartość średnia, σ 2 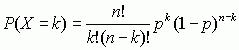 , gdzie p jest liczbą zawartą między 0 i 1 (n! = 1 · 2 · 3 · ... · n); rozkład dwumianowy podaje prawdopodobieństwo zaobserwowania k sukcesów w n niezależnych doświadczeniach (np. w n kolejnych rzutach monetą), z których każde może dać w wyniku sukces z prawdopodobieństwem p;
, gdzie p jest liczbą zawartą między 0 i 1 (n! = 1 · 2 · 3 · ... · n); rozkład dwumianowy podaje prawdopodobieństwo zaobserwowania k sukcesów w n niezależnych doświadczeniach (np. w n kolejnych rzutach monetą), z których każde może dać w wyniku sukces z prawdopodobieństwem p; 
