gier teoria
Encyklopedia PWN
Teoria gier bada te rodzaje gier, w których gracze mają możność świadomego wyboru jednej spośród dostępnych dla siebie akcji. W zakres badań teorii gier wchodzi większość gier rozrywkowych i sportowych, jak brydż, szachy, domino, a także gry wojenne. Najważniejsze zastosowania teoria gier znajduje w ekonomii, naukach politycznych, teorii organizacji, biologii, psychologii, wojskowości, a także w etyce. Teoria gier jest używana do studiowania tak różnorodnych problemów, jak zachowanie firm na rynku, formowanie programów przez partie polityczne, ocena siły głosowania wyborcy lub grupy wyborców, walka gatunków o przetrwanie, ewolucja zachowań społecznych u zwierząt (kooperacja, rywalizacja, altruizm).
„Grę” jako opis sytuacji konfliktowej odróżnia się od opisu konkretnego przebiegu danej gry, zwanej rozgrywką lub partią. Zasadą prowadzenia gry przez każdą z uczestniczących stron jest osiągnięcie maksimum spodziewanego zysku, wyrażanego w tzw. jednostkach użyteczności (niekoniecznie jednostkach monetarnych, a np. w punktach — jak w grze w szachy). Stronę biorącą udział w grze i związaną w danej grze wspólnotą interesów nazywa się graczem (pojęcia tego nie należy personalizować, np. brydż jest w teorii gier grą dwuosobową). Zależnie od liczby graczy gry dzielą się na jednoosobowe (np. pasjans), dwuosobowe i wieloosobowe. Gra dwuosobowa o sumie zero jest grą, w której bierze udział 2 graczy, przy czym dla każdego wyboru strategii zysk jednego z graczy równa się stracie drugiego (tzn. suma wypłat jest równa zeru — stąd nazwa). Grę, w której gracz I ma możność wyboru jednej spośród m możliwych strategii A1, A2,... , Am, a II — jednej spośród n możliwych strategii B1, B2,... , Bn można przedstawić w postaci tablicy (dla przykładu przyjęto m = 3, n = 4), gdzie liczba aij stojąca na przecięciu i -tego wiersza i j-ej kolumny (np. a12 = 3, a34 = 2 itd.) oznacza zysk gracza I (i zarazem stratę gracza II); tablicę taką nazywa się macierzą gry (lub macierzą wypłat).
Chcąc zagwarantować sobie największy zysk (najmniejszą stratę) niezależnie od gry przeciwnika, gracz I powinien rozważyć swoje minimalne zyski przy zagraniu strategii A1, A2, A3 i wybrać tę strategię, przy której ten minimalny zysk jest największy (w ostatniej kolumnie liczby 1, –10, –1 oznaczają właśnie te minimalne wygrane gracza I). Podobnie gracz II powinien rozważyć maksymalne straty przy zagraniu strategii B1, B2, B3, B4 i wybrać tę strategię, przy której ta maksymalna strata jest najmniejsza (w ostatnim wierszu liczby 6, 3, 1, 5 oznaczają właśnie te maksymalne straty gracza II). Taka zasada gry nazywa się zasadą minimaksu. W podanym przykładzie najlepszą strategią dla gracza I jest A1 (wygrana 1), a dla gracza II B3 (przegrana 1). Liczbę 1 nazywa się tu (podobnie w ogólnym przypadku) wartością gry. W ogólnym przypadku gracz I może sobie zagwarantować wygraną równą co najmniej 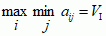 , a gracz II — nieprzegranie więcej niż
, a gracz II — nieprzegranie więcej niż 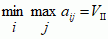 ; jeżeli VI = VII = V, to liczbę V nazywa się czystą wartością gry, a samą grę — zamkniętą; element
; jeżeli VI = VII = V, to liczbę V nazywa się czystą wartością gry, a samą grę — zamkniętą; element 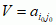 , który jest najmniejszy w swoim wierszu i największy w swojej kolumnie nazywa się punktem siodłowym macierzy gry; gry, które nie mają punktu siodłowego nazywają się otwartymi. Teoria gier rozwinęła się w latach 30. XX w.; jej twórcą był J. von Neumann (Theory of Games and Economic Behavior, 1944, wspólnie z O. Morgensternem). Do rozwoju teorii gier przyczynili się również J. Nash, J. Harsanyi i R. Selten (1994 otrzymali Nagrodę Nobla w dziedzinie ekonomii), Th. Schelling, Gillies, L. Shapley, W. Vickrey (1996 otrzymał Nagrodę Nobla m.in. za zainicjowanie teorii aukcji).
, który jest najmniejszy w swoim wierszu i największy w swojej kolumnie nazywa się punktem siodłowym macierzy gry; gry, które nie mają punktu siodłowego nazywają się otwartymi. Teoria gier rozwinęła się w latach 30. XX w.; jej twórcą był J. von Neumann (Theory of Games and Economic Behavior, 1944, wspólnie z O. Morgensternem). Do rozwoju teorii gier przyczynili się również J. Nash, J. Harsanyi i R. Selten (1994 otrzymali Nagrodę Nobla w dziedzinie ekonomii), Th. Schelling, Gillies, L. Shapley, W. Vickrey (1996 otrzymał Nagrodę Nobla m.in. za zainicjowanie teorii aukcji).
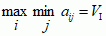 , a gracz II — nieprzegranie więcej niż
, a gracz II — nieprzegranie więcej niż 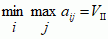 ; jeżeli VI = VII = V, to liczbę V nazywa się czystą wartością gry, a samą grę — zamkniętą; element
; jeżeli VI = VII = V, to liczbę V nazywa się czystą wartością gry, a samą grę — zamkniętą; element 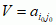 , który jest najmniejszy w swoim wierszu i największy w swojej kolumnie nazywa się punktem siodłowym macierzy gry; gry, które nie mają punktu siodłowego nazywają się otwartymi. Teoria gier rozwinęła się w latach 30. XX w.; jej twórcą był J. von Neumann (Theory of Games and Economic Behavior, 1944, wspólnie z O. Morgensternem). Do rozwoju teorii gier przyczynili się również J. Nash, J. Harsanyi i R. Selten (1994 otrzymali Nagrodę Nobla w dziedzinie ekonomii), Th. Schelling, Gillies, L. Shapley, W. Vickrey (1996 otrzymał Nagrodę Nobla m.in. za zainicjowanie teorii aukcji).
, który jest najmniejszy w swoim wierszu i największy w swojej kolumnie nazywa się punktem siodłowym macierzy gry; gry, które nie mają punktu siodłowego nazywają się otwartymi. Teoria gier rozwinęła się w latach 30. XX w.; jej twórcą był J. von Neumann (Theory of Games and Economic Behavior, 1944, wspólnie z O. Morgensternem). Do rozwoju teorii gier przyczynili się również J. Nash, J. Harsanyi i R. Selten (1994 otrzymali Nagrodę Nobla w dziedzinie ekonomii), Th. Schelling, Gillies, L. Shapley, W. Vickrey (1996 otrzymał Nagrodę Nobla m.in. za zainicjowanie teorii aukcji). 

