Poissona proces

Poissona proces,

mat. proces stochastyczny (N_t)_{t ≥ 0}, którego przyrosty są niezależnymi zmiennymi losowymi o rozkładzie Poissona (rozkład zmiennej losowej): dla t > s, N_t − N_s ma rozkład Poissona z parametrem λ(t − s), czyli P(N_t − N_s = k) = 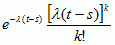, dla k = 0, 1, 2, ...;

współczynik λ > 0 nazywa się intensywnością p.P. Trajektorie p.P. są niemalejącymi funkcjami schodkowymi o skokach równych 1; odcinki czasu między kolejnymi skokami trajektorii stanowią rodzinę niezależnych zmiennych losowych o wspólnym rozkładzie wykładniczym z parametrem λ, równym intensywności procesu (im większe λ, tym skoki następują częściej). Zjawiska, które ewoluują zgodnie z p.P, to np.: liczba roszczeń napływających do danej firmy ubezpieczeniowej, liczba klientów zgłaszających się do stanowiska obsługi, liczba zgłoszeń do centrali telefonicznej, liczba cząstek radioaktywnych emitowanych przez ciało promieniotwórcze. P.P., stosunkowo prosty w opisie mat., może być także używany jako punkt wyjścia do konstrukcji procesów bardziej złożonych.