korelacja
mat. wzajemne powiązanie, współzależność rozważanych zjawisk lub obiektów;
[łac.],
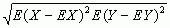 ; dzięki temu podzieleniu współczynnik korelacji jest zawsze liczbą z przedziału [−1, 1] — wartość 1 lub −1 przyjmuje, gdy między rozważanymi zmiennymi losowymi istnieje funkcyjna zależność liniowa; gdy przyjmuje wartość 0, rozważane zmienne losowe nazywa się nieskorelowanymi. W przypadku, gdy obie zmienne losowe X i Y mają rozkład normalny, współczynnik korelacji jest miarą zależności (a nie tylko zależności liniowej) między tymi zmiennymi losowymi; jest równy zeru wtedy i tylko wtedy, gdy te zmienne losowe są niezależne; w ogólnym przypadku jednak tak nie jest — jeżeli np. zmienna losowa X ma rozkład symetryczny względem zera, a Y = X 2, to współczynnik korelacji zmiennych losowych X i Y jest równy zeru. Gdy rozważa się układy wielu zmiennych losowych, współzależność liniowa danych 2 zmiennych losowych oraz współzależność danej zmiennej losowej i pewnego zespołu zmiennych losowych są mierzone, odpowiednio, współczynnikiem korelacji cząstkowej i współczynnikiem korelacji wielokrotnej. Gdy współzależność badanych zmiennych losowych jest oceniana na podstawie próby statystycznej, wszystkie wymienione współczynniki korelacji znajdują zastosowanie przede wszystkim w sytuacji, w której rozważane zmienne losowe mają rozkłady normalne. W innych sytuacjach stosuje się odpowiednie współczynniki statystyki nieparametrycznej, głównie współczynniki korelacji rangowej Spearmana i Kendala. Współzależność zmiennych losowych X(t) i X(t + τ) w procesie stochastycznym X(t) jest opisywana za pomocą autokorelacyjnej funkcji tego procesu.
; dzięki temu podzieleniu współczynnik korelacji jest zawsze liczbą z przedziału [−1, 1] — wartość 1 lub −1 przyjmuje, gdy między rozważanymi zmiennymi losowymi istnieje funkcyjna zależność liniowa; gdy przyjmuje wartość 0, rozważane zmienne losowe nazywa się nieskorelowanymi. W przypadku, gdy obie zmienne losowe X i Y mają rozkład normalny, współczynnik korelacji jest miarą zależności (a nie tylko zależności liniowej) między tymi zmiennymi losowymi; jest równy zeru wtedy i tylko wtedy, gdy te zmienne losowe są niezależne; w ogólnym przypadku jednak tak nie jest — jeżeli np. zmienna losowa X ma rozkład symetryczny względem zera, a Y = X 2, to współczynnik korelacji zmiennych losowych X i Y jest równy zeru. Gdy rozważa się układy wielu zmiennych losowych, współzależność liniowa danych 2 zmiennych losowych oraz współzależność danej zmiennej losowej i pewnego zespołu zmiennych losowych są mierzone, odpowiednio, współczynnikiem korelacji cząstkowej i współczynnikiem korelacji wielokrotnej. Gdy współzależność badanych zmiennych losowych jest oceniana na podstawie próby statystycznej, wszystkie wymienione współczynniki korelacji znajdują zastosowanie przede wszystkim w sytuacji, w której rozważane zmienne losowe mają rozkłady normalne. W innych sytuacjach stosuje się odpowiednie współczynniki statystyki nieparametrycznej, głównie współczynniki korelacji rangowej Spearmana i Kendala. Współzależność zmiennych losowych X(t) i X(t + τ) w procesie stochastycznym X(t) jest opisywana za pomocą autokorelacyjnej funkcji tego procesu.