Idee nowej geometrii przedstawił N. Łobaczewski 1826, a 1829/30 rozwinął je w pracy
O naczałach gieomietrii. W 1832 ukazała się praca J. Bólyaia o analogicznej treści. Niesprzeczność nowej geometrii ostatecznie stwierdzono 1868–70. W planimetrii hiperbolicznej rozważa się tzw. płaszczyznę Łobaczewskiego, tj. płaszczyznę, na której jest spełniony nie aksjomat Euklidesa, lecz aksjomat Łobaczewskiego; na płaszczyźnie tej określa się linie proste, odległości, kąty, ruchy figur itp.; analogiczną geometrię rozwija się w przestrzeni Łobaczewskiego (stereometria hiperboliczna). W 1868 E. Beltrami zauważył, że geometria części płaszczyzny Łobaczewskiego pokrywa się z geometrią wewnętrzną na powierzchniach o stałej ujemnej
krzywiźnie (np. na tzw.
pseudosferze) — rolę prostych odgrywają na nich
geodezyjne. W 1871 F. Klein skonstruował model całej płaszczyzny Łobaczewskiego; w modelu tym rolę płaszczyzny Łobaczewskiego odgrywa wnętrze koła (na zwyczajnej płaszczyźnie euklidesowej), rolę prostych — cięciwy bez końców, a rolę ruchów — dowolne przekształcenia koła w siebie, przeprowadzające cięciwy w cięciwy; w modelu tym odległość między punktami
P i
Q określa się wyrażeniem
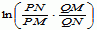
. Inny model geometrii hiperbolicznej podał później H. Poincaré. Geometrię hiperboliczną można również zdefiniować czysto analitycznie jako jedną z tzw. geometrii riemannowskich, ściślej — jako geometrię riemannowską przestrzeni o stałej ujemnej krzywiźnie (
Riemanna geometrie). Wszystkie twierdzenia geometrii euklidesowej, niezależne od aksjomatu o równoległych, są prawdziwe również w geometrii hiperbolicznej (zespół takich twierdzeń stanowi treść tzw.
geometrii absolutnej). W geometrii hiperbolicznej suma kątów dowolnego trójkąta na płaszczyźnie Łobaczewskiego jest mniejsza od π, a 2 trójkąty są równe, jeżeli mają równe kąty (kąty bowiem określają już boki). Im mniejszy rozważa się obszar na płaszczyźnie (lub w przestrzeni) Łobaczewskiego, tym mniejsze są różnice między geometrią hiperboliczną a geometrią Euklidesa. Pojawienie się geometrii hiperbolicznej miało duże znaczenie dla dalszego rozwoju matematyki, głównie dla badań nad aksjomatyką teorii matematycznych. Geometria hiperboliczna znalazła liczne zastosowania zarówno w samej matematyce (np. w obliczaniu całek oznaczonych, w teorii funkcji automorficznych), jak i w fizyce (zwłaszcza w teorii względności).

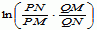 . Inny model geometrii hiperbolicznej podał później H. Poincaré. Geometrię hiperboliczną można również zdefiniować czysto analitycznie jako jedną z tzw. geometrii riemannowskich, ściślej — jako geometrię riemannowską przestrzeni o stałej ujemnej krzywiźnie (
. Inny model geometrii hiperbolicznej podał później H. Poincaré. Geometrię hiperboliczną można również zdefiniować czysto analitycznie jako jedną z tzw. geometrii riemannowskich, ściślej — jako geometrię riemannowską przestrzeni o stałej ujemnej krzywiźnie (
