Euklidesa postulat równoległości, aksjomat równoległości, pewnik Euklidesa,
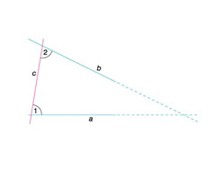
mat. ostatni z pięciu postulatów podanych przez Euklidesa w pierwszej księdze jego Elementów; głosi on: jeśli na płaszczyźnie prosta c, przecinająca dwie inne proste a i b, tworzy z nimi kąty wewnętrzne o sumie mniejszej od 2 kątów prostych (tzn. 180°), to proste a i b przecinają się po tej samej stronie c, po której leżą te kąty;
Euklidesa postulat równoległości
Encyklopedia PWN
w powszechnie obecnie przyjętym sformułowaniu J. Playfaira (1795) postulat równoległości Euklidesa brzmi: jeżeli a oznacza dowolną prostą, A — dowolny punkt nie leżący na a, to w płaszczyźnie wyznaczonej przez a i A istnieje co najwyżej jedna prosta przechodząca przez A i nie przecinająca a. Postulat równoległości Euklidesa jest równoważny twierdzeniu, że suma kątów w trójkącie wynosi 180°, jak też, że na trójkącie można opisać okrąg; postulat ten jest istotny dla geometrii euklidesowej; jego zaprzeczenie prowadzi do geometrii nieeuklidesowych.