krzywizna

krzywizna,

mat. wspólne określenie wielu charakterystyk (liczbowych, wektorowych, tensorowych itp.) opisujących własności obiektów rozważanych w geometrii różniczkowej;

krzywizna krzywej płaskiej wyraża stopień jej odchylenia od prostej. Jeżeli krzywa płaska L jest gładka (tzn. taka, że w każdym swym punkcie ma określoną styczną), to jej krzywiznę w punkcie P określa się następująco: na krzywej L wybiera się drugi punkt Q, którego odległość od punktu P, liczona wzdłuż tej krzywej, wynosi Δs (długość łuków liczy się od jakiegoś dowolnie ustalonego punktu O na krzywej). Styczne w punktach P i Q tworzą kąt Δα, odpowiadający odległości Δs. 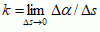Stosunek Δα/Δs charakteryzuje średnie zakrzywienie części PQ krzywej L — granicę k tego punktu, czyli (tzn. gdy punkt Q przybliża się po krzywej L do punktu P) nazywa się krzywizną krzywej L w punkcie P. Jeśli krzywa płaska dana jest równaniem y = f(x), to jej krzywiznę oblicza się wg wzoru: 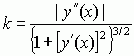; np. okrąg o promieniu r ma w każdym swym punkcie stałą krzywiznę równą k = 1/r. W każdym punkcie P krzywej płaskiej gładkiej można zbudować okrąg do niej styczny, którego krzywizna w punkcie styczności P będzie równa krzywiźnie danej krzywej w tymże punkcie (taki okrąg nazywa się okręgiem lub kołem krzywizny). Promień R = 1/k tego okręgu nazywa się promieniem krzywizny krzywej w punkcie P, a jego środek — środkiem krzywizny. Teoria krzywizny i skręcenia krzywej znajduje zastosowanie m.in. w mechanice teoret. w opisie krzywoliniowych ruchów zmiennych. Pojęcie krzywizny uogólnia się na powierzchnie 2-wymiarowe, a także na przestrzenie wielowymiarowe.