punkt

punkt

[łac.],

mat. w aksjomatycznym ujęciu geometrii — jedno z pojęć pierwotnych (podobnie jak prosta i płaszczyzna); w matematyce współczesnej p. (lub elementami) są nazywane różnego rodzaju przedmioty badań mat., tworzące rozmaite zbiory (przestrzenie);

np. w trójwymiarowej przestrzeni euklidesowej punktem nazywa się uporządkowaną trójkę liczb rzeczywistych (x₁, x₂, x₃); w różnych działach matematyki występują punkty o specjalnych nazwach: 1) punkt P powierzchni z = f(x, y) nazywa się punktem eliptycznym, jeżeli w nim krzywizna K > 0, punktem hiperbolicznym, jeżeli K < 0, punktem parabolicznym, jeżeli K = 0, przy czym krzywizna powierzchni K = (rt – s²)/(1 + p² + q²)², gdzie p = f_x, q = f_y, r = f_xx, s = f_xy, t = f_yy oznaczają pochodne cząstkowe funkcji f(x, y); 2) punkt skupienia (punkt skupienia zbioru A); 3) punkt przegięcia krzywej y = f(x, y), punkt P(x₀, y₀), dla którego f ″(x₀) = 0 i pierwsza nierówna zeru w punkcie x₀ pochodna jest rzędu nieparzystego (a więc f ″′(x₀) ≠ 0, f^(v)(x₀) ≠ 0 itd.); np. 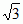punktami przegięcia krzywej y = 1/(1 + x²) są punkty P₁(–¹/₃; ³/₄), oraz punkty P₂(+¹/₃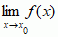; ³/₄), gdyż np. [1/(1 + x²)]″_p1 = 0, a [1/(1 + x²)]″′_p1 ≠ 0; 4) punkt regularny: a) punkt P (x₀, y₀) krzywej y = f(x), w którym istnieje dokładnie jedna styczna o równaniu y – y₀ = f ′(x₀) · (x – x₀); b) punkt P(x₀, y₀, z₀) powierzchni φ(x, y, z) = 0, w którym istnieje dokładnie jedna płaszczyzna styczna o równaniu φ_x(P₀) · (x – x₀) + φ_y(P₀) · (y – y₀) + φ_z (P₀) · (z – z₀) = 0, gdzie φ_x(P₀) itd. oznaczają pochodne cząstkowe funkcji φ obliczone w punkcie P(x₀, y₀, z₀); 5) punkt osobliwy: a) równania różniczkowego P(x, y)dx + Q(x, y)dy = 0 — punkt (x, y), w którym jednocześnie P(x, y) = 0 i Q(x, y) = 0; b) krzywej F(x, y) = 0 — punkt (x, y), w którym wraz z równością F(x, y) = 0 zachodzą także równości F_x(x, y) = 0 i F_y(x, y) = 0; jeżeli przy tym w punkcie (x, y) wszystkie pochodne cząstkowe funkcji F(x, y) aż do rzędu n – 1 włącznie są równe zeru, lecz nie wszystkie n-te pochodne cząstkowe są równe zeru, to dany punkt osobliwy nazywa się punktem osobliwym n-krotnym; np. punkt (x, y) nazywa się punktem osobliwym dwukrotnym, jeżeli F_xx = F_xy = F_yy = 0; rozróżnia się 3 rodzaje punktów dwukrotnych w zależności od znaku wyróżnika W(x, y) = F_xxF_y – F_xy²: punkt dwukrotny (x₀, y₀) nazywa się punktem rozgałęzienia, gdy W(x₀, y₀) < 0, ostrzem krzywej F(x, y) = 0, gdy W(x₀, y₀) = 0, punktem odosobnionym, gdy W(x₀, y₀) > 0; c) funkcji y = f(x) — taki punkt a, dla którego a = ∞, albo w którym funkcja f(x) staje się nieograniczona (np. punkt 0 dla funkcji f(x) = 1/x²); 6) punkt ciągłości funkcji, dla funkcji y = f(x) punkt x₀ (należący do jej dziedziny), w którym jest spełniona równość f(x₀) = , tzn. w którym wartość funkcji jest równa jej granicy; może on nie być jej punktem różniczkowalności; 7) punkt 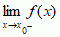nieciągłości funkcji, dla funkcji y = f(x) punkt x₀ (będący punktem skupienia jej dziedziny), w którym funkcja f(x) jest nieciągła; jeżeli istnieją skończone granice oraz 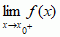i są różne, to punkt x₀ nazywa się punktem nieciągłości pierwszego rodzaju; gdy któraś z powyższych granic jednostronnych (lub obie jednocześnie) jest nieskończona (tj. = ±∞), to odpowiedni punkt x₀ nazywa się punktem nieciągłości drugiego rodzaju; np. dla funkcji y = |x|/x punkt x₀ = 0; 8) punkt zerowy funkcji, dla funkcji y = f(x) liczba x₀ (należąca do jej dziedziny), spełniająca warunek f(x₀ ) = 0; nazywa się go inaczej miejscem zerowym funkcji, np. funkcja y = sinx ma nieskończenie wiele punktów zerowych: x₀ = kπ (k = 0, ±1, ±2, ...); 9) punkt różniczkowalności funkcji, dla funkcji y = f(x) punkt x₀ (należący do jej dziedziny i będący jej punktem ciągłości), w którym istnieje i jest skończona pochodna f ′(x₀); jest on jej punktem ciągłości.