Orbital atomowy opisuje dokładnie stan elektronu jedynie dla atomu wodoru lub jonów wodoropodobnych. Dla tych układów orbital atomowy jest rozwiązaniem równania Schrödingera opisującego ruch elektronu w polu elektrostatycznym jądra przy założeniu, że jądro atomu jest nieruchome i nieskończenie ciężkie; określają go 3 liczby kwantowe: n, l, m. Główna liczba kwantowa n, określająca energię elektronu, może przyjmować wartości n = 1, 2, ...; poboczna liczba kwantowa l, określająca moment pędu elektronu — wartości l = 0, 1, ... , (n – 1); magnetyczna liczba kwantowa m, określająca rzut momentu pędu na wybrany kierunek — wartości –l ≤ m ≤ l (atom). Ograniczenia wartości liczb kwantowych wynikają z konieczności wybrania spośród rozwiązań równania Schrödingera funkcji, których kwadrat modułu można interpretować jako gęstość prawdopodobieństwa. Prawdopodobieństwo znalezienia elektronu, opisanego orbitalu ψ(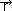 ), w elemencie objętości dV o środku w punkcie r0 jest określone kwadratem modułu funkcji falowej ψ(
), w elemencie objętości dV o środku w punkcie r0 jest określone kwadratem modułu funkcji falowej ψ(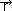 0) pomnożonym przez dV (P = |ψ(
0) pomnożonym przez dV (P = |ψ(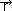 0)|2dV). Graficzną ilustracją orbitalu jest jego kontur — powierzchnia trójwymiarowa obejmująca taki obszar przestrzeni, poza którym prawdopodobieństwo znalezienia elektronu jest niewielkie. Liczby kwantowe charakteryzują wielkość (liczba n), kształt (l) i orientację w przestrzeni (m) konturu orbitalu atomowego; np. kontury orbitali atomowych o liczbie pobocznej l = 0 są kuliste.
0)|2dV). Graficzną ilustracją orbitalu jest jego kontur — powierzchnia trójwymiarowa obejmująca taki obszar przestrzeni, poza którym prawdopodobieństwo znalezienia elektronu jest niewielkie. Liczby kwantowe charakteryzują wielkość (liczba n), kształt (l) i orientację w przestrzeni (m) konturu orbitalu atomowego; np. kontury orbitali atomowych o liczbie pobocznej l = 0 są kuliste. Orbitale atomowe oznacza się symbolami literowymi odpowiadającymi kolejnym wartościom liczby
l: symbolem
s, gdy wartość
l = 0, symbolem
p dla
l = 1,
d dla
l = 2,
f dla
l = 3,
g dla —
l = 4 itd.; z lewej strony symbolu podaje się zwykle wartości
n, z prawej u dołu — wartości
m, np. 2
p0. Zamiast orbitali, którym odpowiada konkretna różna od zera wartość magnetycznej liczby kwantowej, będących funkcjami o wartościach zespolonych, co uniemożliwia ich interpretację graficzną, stosuje się często kombinacje liniowe (tzn. sumy z odpowiednio dobranymi współczynnikami) orbitali atomowych o takich samych liczbach kwantowych
n i
l, a różnych liczbach kwantowych
m. Tak otrzymane orbitale oznacza się z prawej strony u dołu zamiast liczbą
m (nieokreśloną dla nich) indeksem określającym ich orientację w przestrzeni i równania tzw. płaszczyzn węzłowych, tj. płaszczyzn, dla których wartość funkcji falowej jest równa zero.; np. symbol
px oznacza orbital
p leżący wzdłuż osi
x (równy zero, gdy
x = 0, czyli zerujący się na płaszczyźnie
yz),
dxy — orbital
d leżący pomiędzy osiami
x i
y (mający płaszczyzny węzłowe
xz i
yz). Liczby orbitali danego typu wynikają z ograniczeń wartości liczb kwantowych; np. dla liczby kwantowej
n = 1 (stan podstawowy elektronu w atomie wodoru) istnieje tylko jeden orbital 1
s; dla liczby kwantowej
n = 2 jest jeden orbital 2
s i 3 orbital typu
p: 2
p0 (inaczej 2
pz), 2
p−1 i 2
p1 (lub 2
px i 2
py). Jest 2
l + 1 orbitali odpowiadających pobocznej liczbie kwantowej
l (np. 5 orbitali typu
d). Dla układów wieloelektronowych pojedynczy elektron może być opisywany przez orbital jedynie po zastosowaniu tzw.
przybliżenia jednoelektronowego, w którym rozpatruje się stan elektronu poruszającego się w polu elektrostatycznym pochodzącym od jądra (lub jąder w cząsteczce) i uśrednionego rozkładu ładunku pozostałych elektronów. Obliczone w tym przybliżeniu orbitali elektronów w atomach wieloelektronowych przypominają kształtem orbitale dla atomu wodoru i są również określane za pomocą 3 liczb kwantowych
n,
l,
m, ale energia elektronu opisywanego przez orbitale, tzw. energia orbitalna, zależy w tym wypadku nie tylko od głównej liczby kwantowej
n, ale także od pobocznej liczby kwantowej
l. Całkowita energia układu wieloelektronowego zależy od energii orbitalnych i od oddziaływania między elektronami. Najlepsze orbitale (atomowe lub molekularne) opisujące stany elektronów w układzie wieloelektronowym w ramach przybliżenia jednoelektronowego uzyskuje się, rozwiązując równania Hartree’ego i Focka (
Hartree'ego–Focka metoda). Z orbitali można skonstruować całkowitą funkcję falową dla układu wieloelektronowego.
W układzie wieloelektronowym orbital może opisywać tylko 2 elektrony różniące się magnetyczną spinową liczbą kwantową
ms równą +
1/
2 lub –
1/
2 (
Pauliego zakaz); każdemu orbitalowi odpowiadają więc 2 tzw.
spinoorbitale o liczbach kwantowych:
n,
l,
m,
ms, opisujące pojedyncze elektrony.
Orbitale
molekularne (
cząsteczkowe) oblicza się, podobnie jak orbitale atomowe, w przybliżeniu jednoelektronowym i poszukuje się ich zwykle w postaci liniowej kombinacji pewnego skończonego zbioru funkcji, zwanych funkcjami bazy, np. orbitali atomowych atomów tworzących cząsteczkę. Wybór takiej postaci wiąże się z mechanizmem powstawania cząsteczki, tj. wiąże się z faktem, że cząsteczka powstaje z atomów, orbitale molekularne można więc efektywnie opisać za pomocą kombinacji liniowych orbitali atomowych. Orbitale atomowe wchodzące do kombinacji liniowych muszą wykazywać odpowiednią symetrię (np. w przypadku cząsteczki dwuatomowej powinny mieć jednakową symetrię względem osi cząsteczki), a ich udziały w kombinacjach liniowych są duże, jeżeli ich energie orbitalne różnią się nieznacznie i ich kontury nakrywają się w znacznym stopniu. Liczba różnych orbitali molekularnych otrzymanych w wyniku obliczeń jest taka sama, jak liczba orbitali atomowych użytych do utworzenia kombinacji liniowych. Tak otrzymane orbitale molekularne rozciągają się na wszystkie jądra atomowe cząsteczki (są
wielocentrowe i
zdelokalizowane).
Orbitale molekularne, których zapełnienie prowadzi do obniżenia energii elektronów w porównaniu z ich energią w izolowanych atomach, nazywa się orbitalami
wiążącymi, a orbitale, których zapełnienie zwiększa energię elektronów — orbitalami
antywiążącymi. Orbitalowi molekularnemu wiążącemu odpowiada zwiększenie gęstości prawdopodobieństwa znalezienia elektronu w obszarze między jądrami. Liczba elektronów na orbitalach wiążących i antywiążących pozwala wyjaśnić m.in. względną trwałość wiązań chemicznych w cząsteczkach dwuatomowych; np. w najprostszej jednoelektronowej cząsteczce — jonie H
2+, w stanie podstawowym elektron jest opisany orbitalem wiążącym, a wzbudzenie elektronu do stanu opisanego orbitalem antywiążącym powoduje dysocjację cząsteczki na atom H i jon H
+; w dwuelektronowej cząsteczce H
2 obydwa elektrony są opisane orbitalem wiążącym, co powoduje zwiększenie energii wiązania między atomami wodoru (cząsteczka H
2 jest trwalsza od cząsteczki H
2+). W cząsteczce wieloelektronowej mogą również występować orbitale elektronów nie biorących udziału w tworzeniu wiązania, które w cząsteczce w znacznym stopniu zachowują postać, jaką miały w izolowanych atomach; są to tzw. orbitale
niewiążące (orbitale wolnych par elektronowych) oraz orbitale wewnętrznych powłok elektronowych. Do opisu orbitali molekularnych można używać liczb kwantowych jedynie dla niektórych klas cząsteczek, np. dla cząsteczek liniowych, dla których jest określona wartość rzutu momentu pędu elektronu opisywanego orbitalem molekularnym o wartościach zespolonych na oś cząsteczki (scharakteryzowana przez liczbę kwantową
λ, wartości 0, 1, 2, ... są oznaczane odpowiednio symbolami
σ,
π,
δ itd.). Orbitale molekularne klasyfikuje się często także w zależności od symetrii: orbital symetryczny (nie zmieniający kształtu ani znaku) względem odbicia w płaszczyźnie przechodzącej przez oś wiązania nazywa się orbitalem
molekularnym typu σ, a orbital antysymetryczny (zmieniający znak) — orbitalem
molekularnym typu π. Czasami wygodnie jest wykorzystywać przybliżone orbitale molekularne utworzone w taki sposób, aby opisywały elektrony zlokalizowane w określonym fragmencie cząsteczki lub zaangażowane w tworzenie konkretnego wiązania (orbitale
zlokalizowane). Do uproszczonego obliczania orbitali molekularnych można korzystać z tzw.
zhybrydyzowanych orbitali atomowych, szczególnie dogodnych do jakościowego opisu rozkładu ładunku elektronowego wokół atomów tworzących konkretne wiązania, np. z jednego orbitala 2
s i 3 orbitali 2
p atomu węgla można utworzyć 4 orbitale skierowane do naroży czworościanu foremnego (tzw. hybrydyzacja
sp3;
hybrydyzacja), z których z kolei tworzy się orbitale molekularne opisujące wiązania w cząsteczce metanu CH
4. Pozwala to w prosty sposób przewidzieć i wyjaśnić struktury przestrzenne wielu cząsteczek. Podział ładunku elektronowego układu wieloelektronowego na wkłady pochodzące od elektronów opisywanych określonymi orbitalami jest do pewnego stopnia dowolny, ponieważ sens fizyczny ma jedynie całkowity rozkład ładunku elektronowego.
Przypisanie elektronów kolejnym (wg wzrastającej energii) orbitalom z zachowaniem zakazu Pauliego i reguł Hunda pozwala określić konfiguracje elektronowe atomów i cząsteczek, co umożliwia wyjaśnienie wielu ich właściwości, takich jak względna trwałość i długość wiązań w cząsteczkach, oraz istnienie układu okresowego pierwiastków. Znajomość skonstruowanych z orbitali całkowitych funkcji falowych układu wieloelektronowego pozwala określić rozkład gęstości ładunku pochodzącego od wszystkich elektronów oraz strukturę elektronowych widm emisyjnych i absorpcyjnych.
Małgorzata Jeziorska, Piotr Modrak
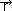 ) określających jego położenie w atomie (orbital atomowy), cząsteczce (orbital molekularny, orbital cząsteczkowy) lub krysztale.
) określających jego położenie w atomie (orbital atomowy), cząsteczce (orbital molekularny, orbital cząsteczkowy) lub krysztale.


