algorytm,
przepis postępowania prowadzący do rozwiązania ustalonego problemu, określający ciąg czynności elementarnych, które należy w tym celu wykonać.
algorytm
Encyklopedia PWN
Algorytm może zawierać definicje obiektów (danych), na których te czynności są przeprowadzane; wykonawcą algorytmu może być człowiek lub urządzenie automatyczne (np. komputer) zdolne do wykonywania poleceń w odpowiedzi na sygnały reprezentujące te polecenia.
Termin algorytm pochodzi od zlatynizowanej formy nazwiska uczonego arabskiego Al-Chuwarizmi (łac. Algorismus, Algorithmus), który w IX w. w Traktacie o rachowaniu na liczbach indyjskich podał przejęty z indyjskich tekstów astronomicznych pozycyjny sposób zapisywania liczb (za pomocą dziesięciu cyfr) i metody wykonywania działań arytmetycznych wykorzystujące ten zapis. Znaczenie terminu algorytm, ograniczone początkowo do przepisów na proste postępowania rachunkowe, uległo następnie rozszerzeniu; wraz z rozwojem informatyki algorytm stał się jej podstawowym pojęciem i obiektem badań (analiza algorytmów).
Cechy algorytmu: 1) możliwość wyrażania go w różnych postaciach (np. w języku naturalnym, w językach programowania, w postaci schematu graficznego); przez zapisanie w języku programowania algorytm staje się programem; 2) możliwość wyrażania go w postaci skończonego ciągu symboli, bez używania zwrotów odwołujących się do analogii, jak „itd.”; 3) realizowalność, tzn. fizyczna możliwość wykonania poleceń; 4) możliwość wielokrotnego wykonywania, na ogół z różnymi danymi. Poprawność algorytm polega na zgodności jego działania i wyników z intencjami twórców, użytkowników; w sensie formalnym oznacza to, że dla ustalonych warunków początkowych, spełnianych przez dane wejściowe, działanie algorytmu zawsze się kończy (tzw. własność stopu), a dane wynikowe spełniają określone warunki końcowe.
Kolejność wykonywania poszczególnych czynności w algorytmie zależy często od danych początkowych i od wyników pośrednich; określone fragmenty algorytmu mogą być wielokrotnie powtarzane (iteracja, rekurencja). Rozróżnia się algorytmy sekwencyjne, w których rozpoczęcie kolejnej czynności musi być poprzedzone zakończeniem poprzedniej, oraz algorytmy niesekwencyjne, w których pewne czynności mogą być wykonywane równocześnie (współbieżność).
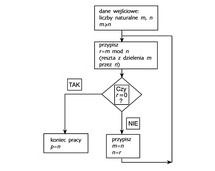
Klasycznym algorytmem, odkrytym w IV w. p.n.e., jest algorytm Euklidesa, służący do obliczania największego wspólnego dzielnika (NWD) dwóch liczb naturalnych m i n (m > 0 i m ≥ n):
Czynność 1: sprawdź, czy n = 0; jeśli tak, to zakończ wykonywanie algorytmu — szukanym NWD jest m; jeśli nie, przejdź do czynności 2. Czynność 2: oblicz resztę z dzielenia m przez n, oznacz ją przez r i przejdź do czynności 1, ale z innymi liczbami: n teraz równym r i m równym poprzedniej wartości n.
Jest to algorytm poprawny dzięki następującemu twierdzeniu arytmetyki: gdy m > 0, to NWD liczb m i n dla n = 0 jest równy m, a dla n > 0 jest równy NWD liczb n i r, gdzie r jest resztą z dzielenia m przez n. Algorytm zakończy działanie, gdyż ciąg reszt obliczanych w kolejnych wykonaniach czynności 2 jest malejący, a każdy malejący ciąg liczb naturalnych jest skończony.
Cechą decydującą dla praktycznej przydatności algorytmu jest jego złożoność obliczeniowa (zwana też kosztem algorytmu), będąca miarą zasobów (np. czasu procesora, pamięci operacyjnej) potrzebnych do rozwiązania za pomocą algorytmu zadania określonego rozmiaru (rozmiarem zadania jest np. długość ciągu liczb do posortowania). Złożoność czasowa algorytmu to funkcja przyporządkowująca rozmiarowi zadania liczbę wykonywanych kolejno w czasie jego rozwiązywania operacji jednostkowych, np. mnożeń, porównań, najbardziej wpływających na czas wykonania algorytmu. Złożoność pamięciowa algorytmu to funkcja przyporządkowująca rozmiarowi zadania maksymalną liczbę komórek pamięci zajętych jednocześnie w trakcie wykonywania algorytmu. Zwykle wyznacza się tzw. rząd złożoności: np. najlepsze algorytmy sortowania mają złożoność czasową rzędu nlogn. Ustalona teoretycznie minimalna złożoność obliczeniowa algorytmu umożliwiającego rozwiązanie zadania określonego typu jest nazywana złożonością zadania.
W podstawach matematyki algorytm jest pojęciem służącym do formułowania i badania rozstrzygalności problemów i teorii. W tym celu pojęcie algorytmu zostało ściśle określone matematycznie. W najbardziej znanej formalizacji algorytmu wykorzystuje się pojęcie maszyny Turinga.
Bibliografia
N. WIRTH Algorytmy + struktury danych = programy, Warszawa 1980;
L. BANACHOWSKI, A. KRECZMAR Elementy analizy algorytmów, Warszawa 1982.
A.V. AHO, J.E. HOPCROFT, J.D. ULLMAN Projektowanie i analiza algorytmów komputerowych, Warszawa 1983;
D. HAREL Rzecz o istocie informatyki — algorytmika, Warszawa 1992.